Simpson azalpena [2/3]
Bigarren urratsa
Aurreko programa aberastuz, jarraian eskaintzen den programan integralaren kalkulua egiten da baina Simpson erregelaren koefizienteak aintzat hartu gabe. Ikus daitekeen bezala IntegralaKalkulatu prozedura barruan x ardatzeko puntuak kontrolatzen dira, eta bakoitzeko dagokion y = f(x) ordenatua kalkulatzen da.
Ordenatuaren kalkulua fnrBaloratu funtzioaren bitartez lortzen da. Funtzio horrek balio erreal bat hartzen du, x koordenatua, eta balio erreal bat itzultzen du: x koordenatu horri dagokion y ordenatua. Polinomioaren 6 eta -4 koefizienteak konstanteak dira eta ez zaizkio fnrBaloratu funtzioari parametro bezala pasatu behar.
Hau da ariketaren iturburu-programa, ikonoaren gainean sakatu programa hartzeko:
Eta hau da programa exekutatzean ateratzen dena:
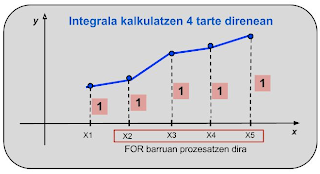
Irudi honetan erakusten da nola kontrolatzen diren x ardatzeko puntuak IntegralaKalkulatu prozedura barruan. Lehena FOR kanpoan prozesatzen da eta gainerakoak FOR barruan prozesatzen dira. Puntu guztientzat y = f(x) ordenatuak lortzen dira eta ez denez koefizienterik aintzat hartzen bakoitzaren koefizientea 1 da.
Ez joan azalpenaren hirugarren urratsera aurreko dena erabat ulertu eta menperatu arte.
Bigarren urratsa
Aurreko programa aberastuz, jarraian eskaintzen den programan integralaren kalkulua egiten da baina Simpson erregelaren koefizienteak aintzat hartu gabe. Ikus daitekeen bezala IntegralaKalkulatu prozedura barruan x ardatzeko puntuak kontrolatzen dira, eta bakoitzeko dagokion y = f(x) ordenatua kalkulatzen da.
Ordenatuaren kalkulua fnrBaloratu funtzioaren bitartez lortzen da. Funtzio horrek balio erreal bat hartzen du, x koordenatua, eta balio erreal bat itzultzen du: x koordenatu horri dagokion y ordenatua. Polinomioaren 6 eta -4 koefizienteak konstanteak dira eta ez zaizkio fnrBaloratu funtzioari parametro bezala pasatu behar.
Hau da ariketaren iturburu-programa, ikonoaren gainean sakatu programa hartzeko:
Eta hau da programa exekutatzean ateratzen dena:
Irudi honetan erakusten da nola kontrolatzen diren x ardatzeko puntuak IntegralaKalkulatu prozedura barruan. Lehena FOR kanpoan prozesatzen da eta gainerakoak FOR barruan prozesatzen dira. Puntu guztientzat y = f(x) ordenatuak lortzen dira eta ez denez koefizienterik aintzat hartzen bakoitzaren koefizientea 1 da.
Ez joan azalpenaren hirugarren urratsera aurreko dena erabat ulertu eta menperatu arte.
Última modificación: martes, 25 de junio de 2013, 13:10