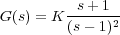 (9.1)
(9.1)Se estudia un método de análisis y diseño que permite conocer la evolución geométrica de los polos del sistema de control en lazo cerrado según un parámetro del mismo varíe su valor.
La dinámica de un sistema de control en lazo cerrado está intimamente ligada con la situación de los polos de su función de transferencia, o lo que es lo mismo, la distribución de las raíces de su ecuación característica en el plano s. Este hecho proporciona un método tanto de análisis como de diseño en Ingeniería de Control. Por un lado, un problema típico de análisis consiste en estudiar como cambia la dinámica o comportamiento de un sistema cuando se produce una modificación en el valor de uno o varios de los parámetros que lo definen. Por otro lado, un problema típico de diseño es estudiar la influencia de alguno de los parámetros del controlador en la dinámica del sistema en lazo cerrado y ajustar el valor de dicho parámetro para obtener el comportamiento deseado en el sistema.
Para cualquiera de los dos problemas es útil determinar el cambio de situación en el plano s de las raíces de la ecuación característica cuando varía el valor de algún parámetro del sistema de control (sea de la propia planta, de la realimentación o del controlador). Consideremos, por ejemplo, un sistema de control con realimentación unitaria negativa y con la siguiente función de transferencia en la cadena directa:
La ecuación característica en lazo cerrado (1 + G(s) = 0) será, por lo tanto:
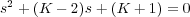
y sus dos raíces, o polos
del sistema en lazo cerrado, son s1,s2 = 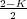 ±
±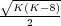 . En el
estudio de la posición de dichas raíces, y la naturaleza de las mismas,
cuando el parámetro K varía entre -∞ y +∞ se dan los siguientes casos:
. En el
estudio de la posición de dichas raíces, y la naturaleza de las mismas,
cuando el parámetro K varía entre -∞ y +∞ se dan los siguientes casos:
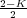 y ω =
y ω = 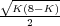 son las
partes real e imaginaria, respectivamente, y j =
son las
partes real e imaginaria, respectivamente, y j = 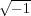 denota la
unidad imaginaria. Eliminando el parámetro K de ambas expresiones e igualando se obtiene la
ecuación de la evolución de dichas raíces en el plano s según varía el parámetro K. Así, la trayectoria descrita por dichas
raíces cuando K varía entre 0 y 8 resulta
ser:
denota la
unidad imaginaria. Eliminando el parámetro K de ambas expresiones e igualando se obtiene la
ecuación de la evolución de dichas raíces en el plano s según varía el parámetro K. Así, la trayectoria descrita por dichas
raíces cuando K varía entre 0 y 8 resulta
ser:
Es decir, una circunferencia de radio dos y centrada en el punto (-1,0). En este intervalo de valores de K se pueden distinguir las siguientes situaciones:
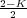 ± jω.
± jω.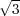 .
.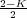 ± jω.
± jω.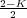 = -3.
= -3.Gráficamente la evolución que experimentan los polos de este sistema en lazo cerrado se puede ver en la Figura 9.1. A partir de dicha figura se puede deducir la siguiente información acerca de la dinámica del sistema en lazo cerrado:
|
El diagrama de la Figura 9.1 se conoce con el nombre de Lugar de las Raíces, y, como se ha explicado anteriormente, se trata de un método gráfico que permite representar la evolución de las raíces de la ecuación característica de un sistema lineal en el plano s cuando varía algún parámetro del mismo, dando de esta forma una medida de la sensibilidad de las raíces con respecto a variaciones en el valor del parámetro que se considere. En definitiva, el estudio del lugar de las raíces de un sistema de control permite conocer la influencia que puede tener un parámetro en la dinámica del mismo, esto es, permite conocer si un posible cambio de valor de un parámetro del sistema (esté en la planta, en la realimentación o en el controlador) afecta mucho o poco en la ubicación de los polos del sistema en lazo cerrado, y en consecuencia, en la dinámica del mismo. En otras palabras, se puede decir que da una medida de la robustez del sistema a variaciones en el valor de un parámetro. Este método fue desarrollado por Evans hacia el año 1948.
Para un análisis más profundo del ejemplo anterior será necesario obtener la función de transferencia en lazo cerrado del sistema. A partir de (9.1) y teniendo en cuenta que H(s) = 1, dicha función de transferencia resulta ser:
Se trata de un sistema de segundo orden con un cero adicional, que es independiente de la ganancia proporcional K. De la gráfica de la Figura 9.1, que representa la evolución geométrica de los polos de la función de transferencia (9.2) cuando el valor de K varía, se observa que en el caso subamortiguado estable (2 < K < 8) al aumentar K aumenta la parte real de los polos complejos conjugados (en valor absoluto) y disminuye el ángulo θ, lo cual implica que en la respuesta transitoria del sistema ante entrada escalón tanto el tiempo de establecimiento como el rebose porcentual disminuye. Respecto a la parte imaginaria de los polos se observa que en un principio aumenta para posteriormente disminuir hasta anularse para K = 8, por lo que el tiempo de pico primero disminuye y después aumenta.
Para obtener los valores exactos de todas las especificaciones anteriores habrá que recordar que el sistema en lazo cerrado (9.2) tiene un cero y por ello se trata de un sistema de segundo orden con un cero adicional.
El Lugar de las Raíces se define como el lugar geométrico que recorren los polos de un sistema en lazo cerrado cuando el valor de la ganancia proporcional K de su correspondiente función de transferencia en lazo abierto varía de 0 a +∞. Relacionado con este concepto, si dicha ganancia varía de 0 a -∞ el lugar geométrico recorrido por los polos del lazo cerrado recibe el nombre de Lugar Inverso de las Raíces. Así mismo, si es otro parámetro diferente a K el que varía de 0 a +∞ (o de 0 a -∞) se denomina Contorno de las Raíces o Lugar de las Raíces Generalizado (Contorno Inverso de las Raíces o Lugar Inverso de las Raíces Generalizado) a la trayectoria seguida por los polos.
Dado el sistema de la Figura 9.2, los polos en lazo cerrado satisfacen la ecuación característica:
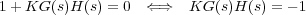
por lo que el punto s0 es polo del sistema en lazo cerrado si satisface ambas condiciones. Notad que ambas condiciones están referidas a la función de transferencia de lazo abierto del sistema.
En el contexto del Lugar de las Raíces el parámetro K es positivo y, por tanto, la condición del argumento queda simplificada a la expresión:
ya que el argumento de un número real positivo es nulo. Entonces, dicha condición únicamente depende de la variable s y bastará, por lo tanto, con realizar la comprobación de si el punto en cuestión s0 cumple la condición del argumento para determinar si dicho punto es polo del sistema en lazo cerrado para algún valor positivo de K. En caso afirmativo, mediante la condición del módulo se podrá conocer el valor concreto de la ganancia proporcional K para la cual el punto s0 es raiz de la ecuación característica. Es decir, los puntos del plano complejo que satisfacen la condición del argumento son polos del sistema para algún valor positivo de K, y por lo tanto, pertenecen al Lugar de las Raíces.
De esta forma, si se
tiene un sistema cuya función de transferencia en lazo abierto es KG(s)H(s) = 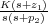 , y se
desea calcular el valor de la ganancia proporcional para la cual un
punto s0 es polo del sistema en lazo cerrado,
entonces es necesario primeramente comprobar que efectivamente dicho
punto puede ser polo del sistema en lazo cerrado para algún valor de la
constante K positiva, esto es, si cumple
la condición del argumento y, por tanto, pertenece al Lugar de las
Raíces.
, y se
desea calcular el valor de la ganancia proporcional para la cual un
punto s0 es polo del sistema en lazo cerrado,
entonces es necesario primeramente comprobar que efectivamente dicho
punto puede ser polo del sistema en lazo cerrado para algún valor de la
constante K positiva, esto es, si cumple
la condición del argumento y, por tanto, pertenece al Lugar de las
Raíces.
La condición del argumento se puede comprobar de dos formas. La primera consiste en realizar directamente el cálculo del argumento del número complejo resultante de sustituir s por s0 en la función de transferencia en lazo abierto, y comprobar si se trata de un número impar de veces 180∘(o π radianes).
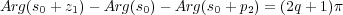
|
La segunda forma consiste en realizar el mismo cálculo de forma gráfica. Si la configuración de polos y ceros de la función de transferencia en lazo abierto es la que se indica en la Figura 9.3, s0 pertenecerá al lugar de las raíces si se cumple:

Si esta condición se verifica, entonces se puede asegurar que el punto s0 es raiz de la ecuación característica del sistema en lazo cerrado para algún valor positivo de K, y mediante la condición del módulo se puede obtener el valor del parámetro K que hace que s0 sea polo del sistema en lazo cerrado. A partir de la Figura 9.3, se deduce que:
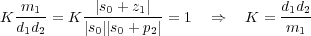
Tal y como se ha planteado este método se puede pensar que el procedimiento para construir el Lugar de las Raíces entraña una búsqueda infinita de puntos s0 que verifiquen la condición del argumento. Afortunadamente no es así. En lo que sigue se va a desarrollar, mediante una serie de reglas de sencillo manejo, un método para la construcción apróximada del Lugar de las Raíces de un sistema.
Se presenta un procedimiento sistemático para obtener una representación aproximada de las trayectorias que siguen las raíces de la ecuación característica de un sistema de control cuando el valor de la ganancia del lazo abierto varía de 0 a +∞.
En primer lugar debe escribirse la ecuación característica en la forma siguiente:
donde K F(s) es la función de transferencia del lazo abierto del sistema. Factorizando F(s) dicha expresión queda:
 (9.6)
(9.6)
En el caso típico de sistema de control realimentado (ver Figura 9.2), F(s) = G(s)H(s), que es la función de transferencia del lazo abierto sin incluir la ganancia ajustable K.
Una vez escrita la ecuación característica de este modo, se aplica el método descrito a continuación para la construcción del Lugar de las Raíces.
El primer paso para la construcción de Lugar de las Raíces consiste en marcar en el plano complejo s la situación de los polos (aspas) y ceros (círculos) de la función de transferencia F(s). A partir de aquí se aplican una serie de reglas que se basan en la relación existente entre los polos y ceros de la función de transferencia F(s) y las raíces de la ecuación característica 9.5 .
A continuación se listan de forma resumida las diferentes reglas que se han de aplicar para la construcción del Lugar de las Raíces.
Como se ha visto en la primera regla, si el exceso polo-cero de la función de transferencia F(s) es diferente de cero, entonces habrá ramas que para grandes valores de la ganancia K tiendan al infinito de forma asintótica. Estas asíntotas son rectas que forman el siguiente ángulo con la parte positiva del eje real:
Las n - m asíntotas se cortan en el eje real a una distancia σ del origen dada por la ecuación:
El ángulo con el que una rama del Lugar de las Raíces sale de un polo de la función de transferencia F(s), o llega a un cero de la misma, se obtiene suponiendo un punto auxiliar s0 perteneciente al Lugar de las Raíces infinitamente próximo al polo o cero en cuestión, y aplicando el principio del argumento.
Así, para obtener el ángulo de salida de la rama que parte del polo -pj queda como única incógnita de la ecuación anterior el argumento del número complejo s0 + pj, que corresponde al ángulo que forma la rama del Lugar de las Raíces que parte del polo -pj con la horizontal (ver Figura 9.4).

Hay que advertir que no todas las soluciones de la ecuación anterior son puntos de dispersión o confluencia del Lugar de las Raíces. Sólo serán validas aquellas soluciones que se corresponden con puntos del plano complejo que satisfacen la condición del argumento de la ecuación característica del sistema.
En el siguiente enlace se encuentra un ejemplo de construcción del Lugar de las Raíces. Se desea conocer las trayectorias descritas por los polos del sistema en lazo cerrado de la Figura 9.5 cuando el valor de la ganancia K del control proporcional varía de 0 a ∞. Además, a partir de dicho resultado se analizará la dinámica del sistema según sea el valor de dicha ganancia.
Como se indicó en la Sección 9.2 si la ganancia proporcional del lazo abierto del sistema es negativa, K < 0, el gráfico que representa la evolución geométrica de los polos en lazo cerrado se denomina Lugar Inverso de las Raíces. La construcción aproximada de dicho gráfico se puede llevar a cabo aplicando un método similar al descrito anteriormente para la obtención del Lugar de las Raíces. Al igual que en dicho caso, las reglas para la construcción del del Lugar Inverso de las Raíces derivan de las condiciones de módulo y argumento (9.3) de la ecuación característica del sistema en lazo cerrado, es decir:

En este caso, al ser
K < 0 se
tiene que Arg = (2q + 1)π y la condición
del argumento será para el Lugar Inverso de las Raíces:
= (2q + 1)π y la condición
del argumento será para el Lugar Inverso de las Raíces:
Por el contrario, la condición del módulo se mantiene igual que cuando K > 0. En consecuencia, las reglas de construcción basadas en la condición del módulo son invariantes con respecto al signo de la ganancia K mientras que aquellas basadas en la condición del argumento cambian con el signo de K. En concreto, las reglas nº 2 (lugar sobre el eje real), nº 4 (ángulos de asíntotas) y nº 5 (ángulos de salida y llegada de las ramas) derivan de la condición del argumento y, por tanto, han de ser cambiadas con respecto a las descritas anteriormente para la construcción del Lugar de las Raíces. El cambio consiste en sustituir el texto “... número impar de ...” por “... número par de ...” en cada una de dichas reglas.
Considerando el diagrama de bloques general para un sistema de realimentación negativa (Figura 9.2), se ha de considerar la construcción del Lugar Inverso de las Raíces, en vez del Lugar de las Raíces (directo), para estudiar la evolución de los polos del lazo cerrado a medida que K varía en los casos siguientes:


Por último, si la realimentación es positiva, en vez de negativa, también sería necesaria la construcción del Lugar Inverso de las Raíces para conocer la evolución de los polos del lazo cerrado cuando K varíe de 0 a ∞, es decir K > 0, en el caso que F(s) = G(s)H(s) tenga ganancia positiva a bajas frecuencias.
Si se desea estudiar la influencia en la dinámica de un sistema en lazo cerrado (situación de sus polos) de un parámetro diferente a la ganancia proporcional K de la cadena directa, se puede utilizar la misma técnica del Lugar de las Raíces vista a lo largo del capítulo con una modificación previa. En este caso, la representación geométrica de la evolución de los polos del sistema en lazo cerrado se denomina Contorno de las Raíces o Lugar de las Raíces Generalizado.
Considérese el sistema de control realimentado de la Figura 9.2 y que se desea estudiar la influencia en la dinámica del sistema de un parámetro α incluido en G(s) y/o en H(s), es decir F(s,α) = G(s)H(s). Al igual que para el Lugar de las Raíces, para la construcción del Contorno de las Raíces se parte de la ecuación característica del sistema, es decir:
y se opera en ella para reescribirla de la siguiente forma:
donde F′(s) es una función de transferencia auxiliar sin ningún sentido físico e independiente del parámetro α. Notad que la ganancia proporcional K del sistema se supone constante y conocida en este caso y está incluida en la función F′(s). Ya que la forma de la ecuación (9.15) es la misma que la de (9.5), cambiando el parámetro α por la ganancia K y la función F′(s) por F(s), para obtener el Contorno de las Raíces del sistema con respecto al parámetro α se aplicarán con F′(s) exactamente las mismas reglas de construcción que se utilizaron con F(s) para obtener el Lugar de las Raíces cuando el parámetro variable era K.
Aunque básicamente el método del Lugar de las Raíces Generalizado permite estudiar el efecto en la dinámica de un sistema de la variación de un solo parámetro, el procedimiento puede extenderse para considerar el efecto de la variación de varios parámetros. Por ejemplo, sea un sistema de control cuya ecuación característica es:
Supóngase que se desea estudiar la influencia de los parámetros α y β en la dinámica del sistema. Para ello, en un principio se puede considerar β = 0, y estudiar el efecto del parámetro α mediante la técnica del Lugar de las Raíces Generalizado reescribiendo la ecuación característica de la forma:

Analizando dicho Contorno de las Raíces se estudia el efecto del parámetro α sobre la dinámica del sistema y se escoge un valor adecuado a los propósitos de diseño, por ejemplo α = α1. Dicho valor se sustituye en la ecuación característica (9.16) y se estudia el efecto del parámetro β reescribiendo la ecuación característica de la siguiente forma:

Analizando este nuevo Contorno de las Raíces se estudia el efecto que tiene en el sistema la variación este parámetro β cuando el parámetro α está fijado al valor α1. Observando este Contorno de las Raíces se seleccionaría un valor β1, adecuado a los propósitos de diseño, para el parámetro β. Si con los valores α1 y β1 seleccionados los propósitos de diseños no son satisfechos adecuadamente, en una nueva iteración se construiría un nuevo Contorno de las Raíces respecto del parámetro α manteniendo fijado el parámetro β en el valor β1 y siguiendo el mismo procedimiento. Despues de varias iteraciones, en las cuales se ha ido estudiando el efecto en la dinámica del sistema de uno de los parámetros fijando anteriormente el otro, se pueden obtener un par de valores, αi y βj, para los parámetros α y β, respectivamente, donde i = j o i = j + 1. Por supuesto, este proceso de elección se puede acortar si el valor de los parámetros está acotado a unos valores que son conocidos. Así, en la primera iteración se partiría de un valor β = β0 ≠ 0 que simplificaría el diseño.
En el siguiente enlace
se encuentra un ejemplo de aplicación del Contorno de las Raíces, aplicado al sistema de la Figura 9.14, en el cual se desea ajustar los parámetros
K y Kd del
bloque de control PD (control proporcional-derivativo) y donde Gp(s) = 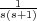 .
.