9.5.1 Ejemplo de Contorno de las Raíces

Sea el sistema de la Figura 9.14 , en el cual se desea ajustar los parámetros K y K_d del bloque de control PD (control proporcional-derivativo). Para ello se va a utilizar la técnica del Lugar de las Raíces, es decir, se trata de un problema de Contorno de las Raíces con dos parámetros.

Figura 9.14:

Diagrama de bloques de un control PD

La función de transferencia en lazo cerrado del sistema es:

$G (s) = Y(s) = -(K-+-Kds-)Gp(s)-- LC R(s) 1+ (K + Kds)Gp (s)$

Por un lado, se observa que el controlador PD introduce un cero en el lazo cerrado del sistema, el cual influye en la dinámica del sistema. Por otro lado, la ecuación característica es:

$1 + (K + Kds )Gp(s) = 0$ (9.17)

Si se desea analizar y diseñar el control mediante la técnica del Lugar de las Raíces, será necesario hacerlo con los dos parámetros K y K_d por separado. Si por la razón que fuera se conoce el valor aproximado de uno de los parámetros, por ejemplo K_d=K_d₁, se considera ese valor para dicho parámetro y se trabaja con la técnica del Lugar de las Raíces para el otro. Si no se pudiese aplicar ninguna información relativa a dicho parámetro, se puede considerar nulo y aplicar la técnica del Lugar de las Raíces para el otro.

En este ejemplo suponemos la segunda situación, es decir, no se dispone de información suficiente para determinar el valor de ninguno de los parámetros del control. Entonces, partimos de K_d=0 y la ecuación característica (9.17) se simplifica a:

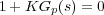
$1+ KGp (s) = 0$

Aplicando la técnica del Lugar de las Raíces a esta ecuación característica se puede obtener un valor para el parámetro proporcional, K=K₁, que pudiera ser definitivo si se cumplen las especificaciones deseadas de diseño, o aproximado si no es así.

Una vez fijado el valor de K=K₁ la ecuación característica (9.17) se puede reescribir:

$1 + (K1 + Kds )Gp(s) = 0 1 + Kd1+sKG1pG(sp)(s) = 0$

y se trataría de realizar un Contorno de las Raíces para el parámetro K_d, ajustando el valor de éste para cumplir todas las especificaciones deseadas para el diseño del control PD. Si no se encontrase un valor adecuado del mismo, se elegiría el valor K_d=K_d₁ que permitiese acercarse a las especificaciones deseadas, y se procedería a repetir el procedimiento estudiado, esto es, se reescribiría la ecuación característica (9.17) con la nueva aproximación del parámetro K_d, es decir:

$1 + (K + Kd1s)Gp(s) = 0 1+ K 1+KGdp(ss)Gp(s) = 0 1$

y se aplicarían las técnicas del Lugar de las Raíces para encontrar un valor adecuado del parámetro K.

Apliquemos este procedimiento para diseñar un controlador PD para un sistema como el de la Figura 9.14 donde G_p(s)=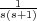 s(s1+1) , de tal forma que las especificaciones deseadas para el sistema en lazo cerrado sean:

El error en régimen estacionario ante entrada rampa sea del 2% del valor de la señal de referencia.
El rebose porcentual de la señal de salida ante entrada escalón sea inferior al 25% del valor de la señal de salida en el permanente.

En primer lugar se procede a un análisis del sistema en lazo cerrado en su conjunto. Se observa que es de tipo 1 ya que la función de transferencia en lazo abierto tiene un polo en el origen. Por ello se deduce que para valores de los parámetros del controlador que hacen el diseño en lazo cerrado estable el sistema presenta:

Error nulo en el permanente ante entrada escalón. Notad que error y señal de error coinciden ya que H(s)=1.
Error finito en el permanente ante entrada rampa unitaria, e_ss=1∕K_v.

Teniendo en cuenta lo anterior, a partir de la primera especificación se puede obtener el valor del primero de los parámetros del controlador:

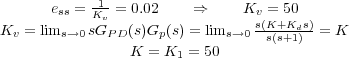
$-1- ess = Kv = 0.02 ⇒ Kvs(=K+5K0ds) Kv = lims→0 sGPD (s)Gp (s) = lims→0-s(s+1)--= K K = K1 = 50$

Valor que queda ya fijado siempre y cuando la primera especificación relativa al régimen estacionario se considere inamovible. Fijando este valor para el parámetro K la ecuación característica queda:

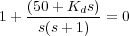
$1 + (50+-Kds)-= 0 s(s+ 1)$

que puede ser reescrita como:

$1 +K ----s-----= 0 ds2 + s +50$ (9.18)

De esta forma se puede estudiar la evolución de los polos en lazo cerrado cuando varia el parámetro K_d (Contorno de las Raíces si K_d>0, o Contorno Inverso si K_d<0). A partir de dicho contorno y teniendo en cuenta el cero que presenta la función de transferencia en lazo cerrado, se puede elegir el valor adecuado del parámetro K_d para que se cumpla la segunda especificación, es decir, %R≤25% ante entrada escalón.

Mediante la aplicación de las reglas de construcción del Lugar de las Raíces, vistas en la Sección 9.3.1, a la función de transferencia auxiliar:

$F ′(s) = ----s----- s2 + s+ 50$ (9.19)

se obtiene el Contorno de las Raíces para el parámetro K_d≥0 (teniendo en cuenta que normalmente es positivo) (Figura 9.15).

Figura 9.15:

Contorno de las raíces para 0 ≤ K_d < ∞.

Antes de elegir una pareja de polos del sistema en lazo cerrado mediante la selección de un valor del parámetro derivativo conviene estudiar primeramente la función de transferencia en lazo cerrado del sistema:

$G (s) = Y-(s) =-----50+-Kds----- LC R (s) s2 + (1+ Kd )s+ 50$ (9.20)

El sistema es de segundo orden con un cero adicional, el introducido por el controlador PD, situado en s=-50∕K_d.

Como método de diseño en un principio se puede no considerar el efecto del cero en la dinámica del sistema centrándose únicamente en la pareja de polos. Este razonamiento puede ser correcto si el cero está lo suficientemente alejado del eje imaginario en comparación con la pareja de polos dominantes, de lo contrario no será muy exacta la aproximación inicial. Así, la función de transferencia en lazo cerrado aproximada será:

$Gaprox(s) = Y-(s) =-------50-------- LC R (s) s2 + (1+ Kd )s+ 50$ (9.21)

Es decir, un sistema típico de segundo orden en el que se ha mantenido la ganancia unitaria del sistema. El cálculo de la ganancia K_d para que este sistema tenga un rebose porcentual del 25% es bien sencillo utilizando la fórmula correspondiente:

$%R = 100e√-1π-δδ2 = 25%$ (9.22)

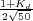con δ= 1+2√K5d0- siendo el coeficiente de amortiguamiento.

Sin embargo, y sin realizar ningún cálculo, es evidente que obteniendo el coeficiente derivativo K_d mediante la fórmula (9.22) el rebose porcentual del sistema real (9.20) será superior al 25% esperado, ya que la presencia del cero aumenta el rebose, y tanto más cuanto más cerca esté del eje imaginario. Así, en un principio no podemos cuantificar esta cercanía, y por ello el aumento del rebose, pero podemos estar seguros que algo sí lo aumentará.

En la práctica se calcula un valor para el parámetro K_d tal que el rebose del sistema de segundo orden sin cero (9.21) sea más pequeño que el deseado. De esta manera se compensa el efecto del aumento de rebose provocado por la presencia del cero adicional. Por ejemplo, se considera que se desea que el sistema aproximado G_LC^aprox(s) tenga un 16% de rebose y mediante la expresión (9.22) se tiene:

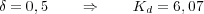
$δ = 0,5 ⇒ Kd = 6,07$

quedando diseñado el controlador PD.

Si se desea realizar el diseño mediante la técnica del Lugar de las Raíces habrá que seguir otro camino, aún cuando en este caso la resolución del problema es mucho más sencilla de la forma anterior. En un primer paso, es necesario elegir una pareja de polos que, si son dominantes y si el sistema es de segundo orden típico, hagan que se cumplan las especificaciones deseadas. En este caso, si el %R deseado es del 16% y si el sistema fuera de segundo orden típico entonces el coeficiente de amortiguamiento según (9.22) quedaría fijado en δ=0,5, y por lo tanto los dos polos de la función de transferencia en lazo cerrado de segundo orden típica serían:

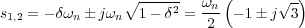
$∘ ------ ( √ -) s1,2 = - δωn ± jωn 1- δ2 = ωn- - 1± j 3 2$

Una vez elegidos los polos en lazo cerrado, estos puntos, para que efectivamente sean polos del sistema en lazo cerrado, deberán pertenecer al Contorno de las Raíces, o lo que es lo mismo deberán cumplir la condición del argumento ( 9.3) de la ecuación característica 9.18, es decir:

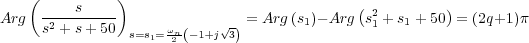
$( ) Arg ----s----- = Arg(s )- Arg (s2 + s + 50) = (2q+1)π s2 + s+ 50 s=s1= ωn2-(- 1+j√3) 1 1 1$

La resolución de esta ecuación determina el valor la constante ω_n y, por tanto, la situación de los polos complejos conjugados deseados para el sistema en lazo cerrado:

$ω = 7,07 ⇒ s = - 3,5± j6,1 n 1,2$

Por último, para obtener el valor del parámetro K_d que hace que los puntos s_1,2 sean polos del sistema en lazo cerrado se utiliza la condición del módulo (9.3) de la ecuación característica 9.18, es decir:

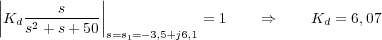
$| | || ----s----|| |Kd s2 + s+ 50|s=s= -3,5+j6,1 = 1 ⇒ Kd = 6,07 1$

De este modo, se obtiene el controlador PD:

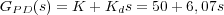
$GPD (s) = K + Kds = 50+ 6,07s$

Si se introduce ahora este controlador, que ha sido calculado para que el sistema aproximado G_LC^aprox(s) (9.21) cumpla la especificación deseada del rebose porcentual, en el sistema real G_LC(s) (9.20) el rebose será mayor al 16% previsto como se explicó anteriormente, y como se comprueba realizando una simulación del comportamiento del sistema. En la Figura 9.16 se observa que el rebose es aproximadamente del 26% que se puede dar por bueno.

Figura 9.16:

Respuesta del sistema real en lazo cerrado con el controlador diseñado

Notad que la función de transferencia en lazo cerrado del sistema controlado (9.20) es:

$G (s) = Y-(s) =--50+-6,07s-- LC R (s) s2 + 7,07s+ 50$

El cero que introduce el control PD está situado en s=-50∕K_d=-8.23, es decir, no está lo suficientemente alejado del eje imaginario respecto de los polos dominantes (s_1,2=-3,5±6,1j) como para despreciar su influencia. De hecho, la presencia de este cero es el que ha subido el rebose del 16%, correspondiente al sistema apróximado de 2º orden sin cero G_LC^aprox(s), al 26%, correspondiente al sistema real G_LC(s).