9.3.2 Ejemplo de construcción del Lugar de las Raíces

Se desea conocer las trayectorias descritas por los polos del sistema en lazo cerrado de la Figura 9.5 cuando el valor de la ganancia K del control proporcional varía de 0 a ∞. Además, a partir de dicho resultado se analizará la dinámica del sistema según sea el valor de dicha ganancia.

Figura 9.5:

Diagrama de bloques de un sistema con control proporcional

Observando el diagrama de bloques, la función de transferencia del lazo abierto del sistema es:

$KG (s)H (s) = KF (s) = K-----(s+-2)------ s(s+ 1)(s2 +2s + 2)$ (9.10)

Asimismo, para el posterior análisis de la dinámica del sistema es necesario calcular la función de transferencia en lazo cerrado, siendo ésta:

$G (s) = ------K-(s+-1)(s+-2)------- LC s(s+ 1)(s2 + 2s+ 2)+ K (s+ 2)$ (9.11)

Se puede observar que en lazo cerrado aparecen dos ceros (el de la cadena directa y el polo de la realimentación) cuyos efectos en la dinámica habrá que tener en cuenta.

En primer lugar para construir el Lugar de las Raíces habrá que marcar en el plano s la situación de los polos (aspas) y ceros (círculos) de la función de transferencia F(s) = G(s)H(s) (9.10). A continuación, se aplican las reglas de construcción vistas en el apartado 9.3.1. Notad que esquemas de control diferentes del mostrado en la Figura 9.5 pero con la misma F(s) tendrán el mismo Lugar de las Raíces que éste ya que el Lugar de las Raíces se construye a partir de la función de transferencia F(s).

Número de ramas, comienzo y final.

Dado que la función de transferencia F(s) tiene 4 polos, la función de transferencia en lazo cerrado tendrá 4 polos y existirán por tanto 4 ramas en el Lugar de las Raíces. Las 4 ramas partirán de los 4 polos de F(s) (que son polos de la función de transferencia en lazo cerrado cuando K = 0):

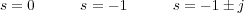
$s = 0 s = - 1 s = - 1± j$

Una de dichas ramas finalizará en el cero de F(s) (que es polo de la función de transferencia en lazo cerrado cuando K tiende a ∞):

$s = - 2$

Las otras tres ramas (exceso polo-cero) irán al infinito siguiendo 3 asíntotas que se calcularán en la regla nº 4.
Lugar sobre el eje real del plano s.

Observando los polos y ceros de la F(s) se concluye que los puntos del eje real que pertenecen al Lugar de las Raíces están incluidos en los intervalos: $⋃ (- ∞,- 2] [- 1,0]$
Simetría
El Lugar de las Raíces es simétrico respecto al eje real.
Asíntotas e intersección de las mismas.

Al ser el exceso polo-cero de F(s) igual a 3 habrá 3 ramas que para grandes valores de la ganancia K tiendan al infinito de forma asintótica. Estas asíntotas son rectas que forman, utilizando la fórmula (9.7), los siguientes ángulos con la parte positiva del eje real: $θ0 = π3 θ1 = π θ2 = 53π$

Las 3 asíntotas se cortan en el eje real a una distancia σ del origen (9.8):

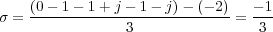
$(0- 1- 1 + j - 1- j)- (- 2) - 1 σ = ------------------------- = --- 3 3$

A dicho punto se le denomina centroide.
Ángulos de salida y llegada de las ramas.
- Ángulo de salida del polo s = 0:
  
  Es evidente que dado que el intervalo pertenece al Lugar de las Raíces, la rama saldrá del origen con ángulo φ = 180∘ = π rad .
- Ángulo de salida del polo s = -1:
  Por la misma razón que el caso anterior el ángulo de salida será φ = 0∘ = 0 rad
- Ángulo de llegada al cero s = -2:
  Dada la pertenencia al Lugar de las Raíces del tramo , el ángulo de llegada será φ = 180∘ = π rad .
- Ángulo de salida del polo s = -1 + j:
  
  Considerando un punto auxiliar s₀ perteneciente al Lugar de las Raíces e infinitamente próximo al polo s = -1 + j (Figura 9.6) y aplicando el principio del argumento ( 9.9) se obtiene:
  
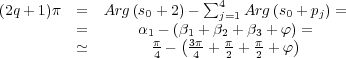
  $∑4 (2q + 1)π = Arg (s0 + 2)- j=1Arg (s0 + pj) = = α1 - (β1( + β2 + β3 + φ))= ≃ π4 - 3π4-+ π2 + π2 + φ$
  
  A partir de dicha expresión, se deduce que el ángulo de salida de la rama que parte de dicho polo es φ = -.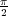
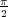- Ángulo de salida del polo s = -1 - j:
  
  Por simetría del Lugar de las Raíces con respecto al eje real, el ángulo de salida de esta rama tiene que ser simétrico al ángulo de salida de la rama del polo complejo conjugado. Por tanto, φ = .
  
  Figura 9.6: Cálculo gráfico del ángulo de salida de la rama que parte del polo s = -1 + j
  
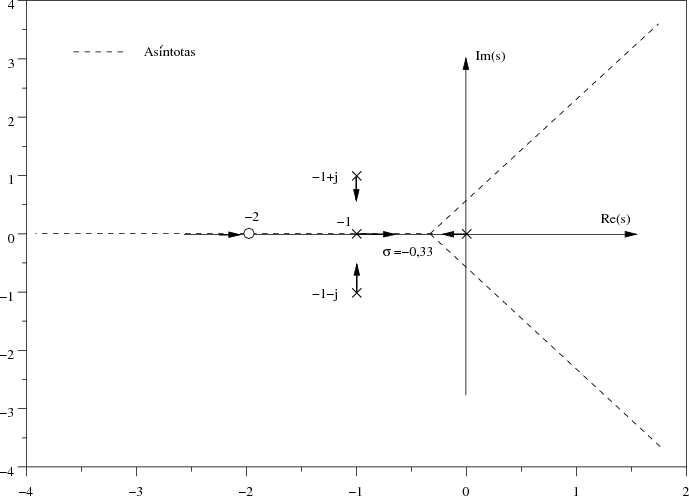
  En la Figura 9.7 se puede observar la construcción del Lugar de las Raíces con las reglas aplicadas hasta este momento.
  
  Figura 9.7: Construcción del Lugar de las Raíces de la Figura 9.5
Puntos de dispersión o confluencia de ramas.

Se observa que al menos han de existir dos puntos de dispersión, uno en el intervalo y otro en . Por un lado, en algún punto del primer intervalo confluirán las dos ramas que finalizan en los puntos s = -2 y s = -∞, y por el otro, en algún punto del segundo intervalo las dos ramas que parten de los puntos s = 0 y s = -1 tendrán que dispersarse.
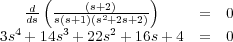
Según la regla nº6 se tiene: $d-( ----(s+2)----) ds s(s+1)(s2+2s+2) = 0 3s4 + 14s3 + 22s2 + 16s+ 4 = 0$

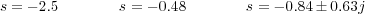
$s = - 2.5 s = - 0.48 s = - 0.84± 0.63j$

A continuación, se comprueba la pertenencia o no de estos puntos al Lugar de las Raíces. Para ello se aplica la condición del argumento de la ecuación característica de sistema en cada uno de dichos puntos. Aquellos puntos que satisfacen dicha condición pertenecen a Lugar de las Raíces y, por tanto, son puntos de confluencia o dispersión. Por último, el valor de la ganancia propocional K para el cual se alcanza un punto de confluencia o dispersión se obtiene aplicando la condición del módulo de la ecuación característica del sistema en dicho punto. De este modo se deduce que:

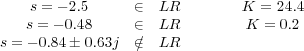
$s = - 2.5 ∈ LR K = 24.4 s = - 0.48 ∈ LR K = 0.2 s = - 0.84± 0.63j ∕∈ LR$

es decir, por un lado, cuando K = 0.2, el polo que sigue la rama que parte del punto s = 0 y el que sigue aquella que parte de s = -1, se encuentran en el punto s = -0.48. Por otro lado, cuando K = 24.4 el polo del sistema que sigue la rama que finaliza en s = -2 y aquel que sigue la rama que finaliza en s = -∞ se encuentran en s = -2.5. Por tanto, s = -0.48 y s = -2.5 son puntos de dispersión o confluencia de ramas del Lugar de las Raíces del sistema.
Intersección con el eje imaginario.
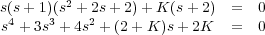
La ecuación característica del sistema es: $s(s + 1)(s2 + 2s+ 2)+ K (s+ 2) = 0 s4 + 3s3 + 4s2 + (2+ K )s+ 2K = 0$

Aplicando la regla de Routh-Hurwitz al polinomio característico se obtiene la tabla de Routh:

$s4 1 4 2K s3 3 2 +K 0 s2 10-K-- 2K 0 1 20-130K--K2 s0 10-K 0 s 2K 0$ (9.12)

Analizando la primera columna se tiene que el rango de estabilidad de la ganancia proporcional K queda fijado en:

$0 < K < 1.7$

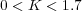
Utilizando los valores límite de la ganancia K y las ecuaciones auxiliares que con ellos se obtienen de la tabla de Routh-Hurwitz, se calculan los puntos de corte de las ramas del Lugar de las Raíces con el eje imaginario. De este modo, se deduce que:

$K = 0 ⇒ s = 0 K = 1.7 ⇒ s = ±1.2 j$

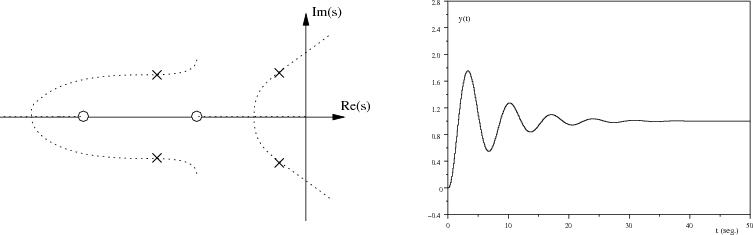
es decir, existen tres puntos de corte con el eje imaginario. Uno de ellos es el punto s = 0 que corresponde al valor K = 0 y es, por tanto, el punto de arranque de una de las ramas del Lugar de las Raíces. Los otros dos puntos, s = ±1.2j, son polos del sistema cuando la ganancia K = 1.7. En este caso, el sistema es críticamente estable ya que hay dos polos en el eje imaginario y otros dos polos estables como se puede deducir de la tabla de Routh 9.12 evaluada cuando K = 1.7. Notad que los coeficientes de la primera columna de dicha tabla son todos positivos excepto el coeficiente de la fila correspondiente a s¹, el cual es nulo.

En definitiva, una vez aplicado el método de construcción del Lugar de las Raíces al ejemplo considerado, se obtiene la representación gráfica del mismo mostrada en la Figura 9.8.

Figura 9.8:

Lugar de las Raíces del sistema de la Figura 9.5

A partir de dicha representación, se puede hacer el análisis de la dinámica del sistema según varíe el valor de la ganancia K del controlador proporcional. Primeramente, es necesario recordar la función de transferencia en lazo cerrado del sistema (9.11) que se estudia:

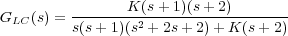
$K (s+ 1)(s+ 2) GLC(s) = --------2------------------ s(s+ 1)(s + 2s+ 2)+ K (s+ 2)$

Analizando tanto la función de transferencia en lazo cerrado como el Lugar de las Raíces de la Figura 9.8 se llegan a las siguientes conclusiones:

La ganancia del sistema en lazo cerrado es unitaria, siempre y cuando sea estable. Esto era evidente, por ser el sistema de tipo 1, y tener la realimentación ganancia unitaria.
En la función de transferencia en lazo cerrado existen dos ceros, uno de los cuales (s = -1) no consta como cero en el Lugar de las Raíces (se trata del polo de la realimentación) pero que tambien influye en la dinámica del sistema. Ambos ceros no dependen de la ganancia K, es decir, son fijos aunque el valor de K varíe.
El rango de estabilidad es:

$0 < K < 1.7$
Dado que los dos polos más alejados (los que recorren las ramas que parten de los puntos s = -1 ± j) son complejos conjugados para valores de la ganancia tal que K < 24,4, y el rango de estabilidad es 0 < K < 1.7, se concluye que la salida del sistema oscila siempre para entrada escalón. Es decir, para el rango de valores de K que garantizan la estabilidad del sistema, la función de transferencia del mismo posee al menos una pareja de polos complejos conjugados.
Los polos complejos conjugados que recorren las ramas que parten de los puntos s = -1 ± j nunca son dominantes.

Figura 9.9:

Enumeración de los 4 polos de la función de transferencia en lazo cerrado

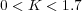
Para analizar más en profundidad el comportamiento del sistema según sea el valor de la ganancia proporcional será necesario estudiar la configuración de polos y ceros en lazo cerrado para varios intervalos de la ganancia proporcional K. Para simplificar la explicación se van a enumerar los polos en lazo cerrado según sea la rama por la que evolucionen, como se puede ver en la Figura 9.9.

Figura 9.10:

Configuración polo-cero en lazo cerrado para 0 < K ≤ 0,2, y respuesta del sistema ante entrada escalón unitario.

0 < K ≤ 0.2: Los polos 1 y 2 son reales, siendo dominante el nº 1. Los otros dos polos estarán en algún punto cercano de los puntos de partida de sus correspondientes ramas (Figura 9.10). Los dos ceros son fijos y situados en s = -1 y s = -2. Además, si el valor de K es muy pequeño el polo real 2 estará lo suficientemente cercano al cero s = -1 como para compensar sus efectos contrarios en la dinámica del sistema. En dicho caso el sistema presenta un polo real dominante y muy cercano al origen, pudiéndose despreciar la influencia del resto de polos y ceros en la dinámica del sistema. Es decir, la respuesta del sistema ante entrada escalón sería muy lenta y sin prácticamente oscilaciones (Figura 9.10 ).

Figura 9.11:
Configuración polo-cero en lazo cerrado para 0,2 < K < 1,7, y respuesta del sistema ante entrada escalón unitario.
0.2 < K < 1.7: Los polos 1 y 2 son complejos conjugados y dominantes. El cero s = -1 está bastante cerca de los polos dominantes, y el resto no estarán excesivamente lejos. Por tanto, la respuesta del sistema ante entrada escalón será oscilante con, previsiblemente, mayores oscilaciones y rebose que un sistema de segundo orden típico (sin ceros) con únicamente los polos 1 y 2 (Figura 9.11).

Figura 9.12: Configuración polo-cero en lazo cerrado para K = 1,7, y respuesta del sistema ante entrada escalón unitario.
K = 1.7: Los polos 3 y 4 siguen estando en algún punto de sus correspondientes ramas, seguramente cerca del punto de partida, mientras que los polos 1 y 2 se colocan en el eje imaginario, convirtiéndose por tanto en un sistema críticamente estable, con una salida oscilatoria no amortiguada ante entrada escalón (Figura 9.12).

Figura 9.13: Configuración polo-cero en lazo cerrado para K > 1,7, y respuesta del sistema ante entrada escalón unitario.
K > 1.7: Los polos 1 y 2 están ya en el semiplano derecho y, por lo tanto, el sistema en lazo cerrado es inestable (Figura 9.13), siendo innecesario un estudio más detallado de la dinámica del sistema.
K ≥ 24.4: Los polos 3 y 4 se convierten en reales, pero al ser el sistema inestable este cambio no supone nada reseñable.