Completion requirements
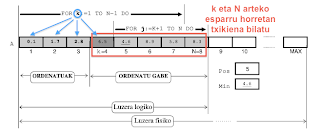
Demagun array dimentsibakar bat dugula (bektore bat) eta bere elementuak zenbaki errealak direla, 0-tik 9-ra bitarteko alde osoa eta dezimal bakarra duten zenbaki errealak alegia. Eskatzen digute array hori ordenatzea txikitik handira. Hauxe litzateke algoritmoaren irudia:
Eskeman ikus daitekeenez k kontagailuaren laugarren iterazioan gaude, ordurako array ordenatuaren lehen hiru elementuak zehaztu dira, eta iterazio honetan aurkituko den minimoa gelaska ilunean kokatuko dugu (k=4 posizioan alegia). Laugarren iterazioari dagokion minimoa bilatzeko, arrayaren ordenatu gabeko aldean begiratu beharra dago eta horretarako j kontagailua erabiliko da.
k=4 iterazioari dagokion minimoa zehazteko Min eta Pos aldagai laguntzaileen bitartez egiten da. Hasiera batean Min aldagaian ordenatu gabeko tartearen lehen elementuaren balioa gordetzen da, hots, Min aldagaian A[k] elementuaren balioa gordetzen da eta Pos aldagaian elementu horri dagokion k posizioa. Hasieraketak egin ondoren, barneko FOR-DO bitartez ordenatu gabeko aldea aztertzen da elementurik txikiena zehaztuz (bere balioa eta bere posizioa zehaztuz). Laugarren iterazioan minimoa zein den jakitean, array ordenatuan dagokion tokira (k=4 posiziora) eraman behar da, horregatik k eta Pos indizedun elementuak elkar trukatu egin behar dira.
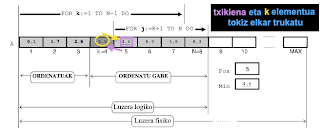
Eskeman ikus daitekeenez k kontagailuaren laugarren iterazioan gaude, ordurako array ordenatuaren lehen hiru elementuak zehaztu dira, eta iterazio honetan aurkituko den minimoa gelaska ilunean kokatuko dugu (k=4 posizioan alegia). Laugarren iterazioari dagokion minimoa bilatzeko, arrayaren ordenatu gabeko aldean begiratu beharra dago eta horretarako j kontagailua erabiliko da.
k=4 iterazioari dagokion minimoa zehazteko Min eta Pos aldagai laguntzaileen bitartez egiten da. Hasiera batean Min aldagaian ordenatu gabeko tartearen lehen elementuaren balioa gordetzen da, hots, Min aldagaian A[k] elementuaren balioa gordetzen da eta Pos aldagaian elementu horri dagokion k posizioa. Hasieraketak egin ondoren, barneko FOR-DO bitartez ordenatu gabeko aldea aztertzen da elementurik txikiena zehaztuz (bere balioa eta bere posizioa zehaztuz). Laugarren iterazioan minimoa zein den jakitean, array ordenatuan dagokion tokira (k=4 posiziora) eraman behar da, horregatik k eta Pos indizedun elementuak elkar trukatu egin behar dira.
Hona hemen iturburu-programa:
Last modified: Tuesday, 25 June 2013, 13:24