| DEFINIZIOA Aintzinako Grezian arrazonamenduaren sistematizazioa lortu zen. Grezia klasikoan geometria aztertzeko axiomak erabiliz egiten zen. Beraz, esate baterako zirkuluaren propietateak ikasteko esperimentuak eta neurketak egin beharrean, grekoek zirkuluaren definizio formala eginez dagokion geometriaren dedukzio-sistema bat eraiki zuten. Era berean, garai hartako pentsatzaileek baliozko arrazonamendua nola egin zitekeen sakonki ikertu zuten. Aristotele filosofoak logika formala sortu zuen eta bere lanek XIX. mendean jarraipena izan zuten. Hona hemen Aristotelen tratatuetan irakur daitekeen adibidea:
Arrazonamendu mota honi modus ponens esaten zaio eta ikus daitekeenez Baldin eta - orduan gakoak erabiltzen ditu. Matematika eta gainerako zientzietan agertzen da arrazonamendu mota hau eta oso emankorra da, baina bada beste arrazonamendu era bat asko erabiltzen dena eta modus tollens bezala ezagutzen dena. Aristotelerekin jarraituz:
Aristotelen lanei jarraipena emanez, George Boole matematikaraiak, 1847 urtean, proposizio-logikaren hedapena lortu zuen. Boolek adierazpen aritmetikoen eta adierazpen logikoen arteko paralelismoa aurkitu zuen, hori dela eta AND eta OR eragile logikoek x eta + eragile aritmetikoekin duten parekotasuna handia dela frogatu zuen. Adierazpen aritmetikoek zenbakiak eta kopuruak maneiatzeko ahalmena dute, modu beretsuan Boole-ren Algebrak proposizioak (esaldiak) zuzentasunez eta doitasunez maneiatzeko ahalmena du. Booleren funtsezko ideia argumentazio logikoak sinboloen bitartez ordezkatzea izan zen. Jarraian ematen diren esaldiak balio bi onartzen dituzte gezurra ala egia, horregatik proposizioak izango dira:
Goian aipaturiko esaldiak proposizioak dira, baina horien maneiaketa errazteko proposizioak sintaxi jakin bat beteko duten aldagai sinbolikoen bitartez ordezkatzen dira, aldagai horien datu-mota Turbo Pascal goimailako lengoaian Boolean deitzen da. Datu-mota boolearren bitartez definituriko konstanteek edo/eta aldagaiek bi balioetatik bat har dezakete. Aldagai edo konstante boolear batek FALSE ala TRUE balio dezake, baina ez besterik. Beraz datu-mota boolearrek duten heina 2 da, eta zentzu fisikorik izan ez arren FALSE balioa TRUE balioa baino txikiagoa da. Nahiz eta bit batekin aski izan, Turbo Pascalek byte bat erreserbatzen du memorian aldagai edo konstante boolear baterako. Horra hor konstante eta aldagai boolearrak definitzeko lerroak:
CONST OK = TRUE ; GEZURRA = FALSE ; VAR Aurkitua, Amaiturik : Boolean ;
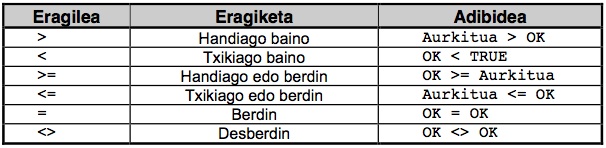
Boolearrak diren datu-motek onartzen dituzten eragiketak bi taldetan sailkatzen dira, batetik eragiketa logikoak deitzen direnak, eta bestetik erlaziozko eragiketa ezagunak. Berriak diren eragile logikoei begirada bat eman diezaiegun:
Besteek, erlaziozko eragileek, esan dugunez zentzu fisikorik ez dute eragigai boolearrekin. Edozein kasutan ere, erlaziozko eragileen bitartez sortzen diren adierazpenak ebaluatzeko FALSE balioa TRUE balioa baino txikiagoa dela gogoratu.
Datu-mota boolearrekin gehien erabiliko ditugun erlaziozko eragileak azken biak izango dira, = eta <> alegia. |
|
BOOLEAN DATU-MOTA ERABILTZEN: ADIERAZPEN BOOLEARRAK
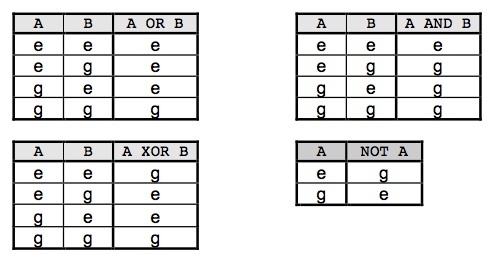
Lau dira Pascal lengoaiaren eragile logikoak, eta aritmetikan eragile aritmetikoak bezala, eragigaiak elkar lotuz adierazpenak eraikitzeko balio dute (adierazpen logikoak7 eragile logikoekin, adierazpen aritmetikoak eragile aritmetikoekin). A eta B eragigai boolearrak izanik, eragile logikoak aplikatu eta ondorioztatzen den adierazpen bakoitzari dagokion emaitza taula batean antolantzen da, horri egi taula esaten zaio. Egi tauletan agertuko diren emaitzak egiazkoak (e) ala gezurrezkoak (g) izan daitezke.
Ikusten denez, NOT eragileak A-ren balioari dagokion aurkakoa lortzen du. Beste eragileek eragigai bi darabiltzate, A AND B adierazpena egia izan dadin eragigai biek TRUE balio behar dute. Bestalde, A OR B disjuntzioa egia izan dadin nahikoa da eragigai bietarik batek TRUE balio izatea.
Disjuntzio arruntarekin batera bada eguneroko hizkuntzan erabiltzen den beste disjuntzio mota bat, disjuntzio elkarbaztertzailea alegia. Amak umeari honela esaten dionean “piszina edo zinema”, bien artean bat aukeratu behar duela ulertzen da, hots, piszinara joan ala bestela zinemara. Argi dagoenez disjuntzio logiko arruntaren egi taulak ez dio disjuntzio elkarbaztertzailearen egoera horri egoki erantzuten, horretarako A XOR B disjuntzioa dago eta duen emaitza egia izango da sarrera biak desberdinak direnean. Lau eragile logiko horien artean hierarkia bat dago, eta operadore aritmetikoen antzera familietan sailka daitezke: ukatzailea logikoa alde batetik, disjuntzio biek batuketaren familia osatzen dute eta konjuntzioa biderkaketa familia litzateke. Adierazpen logikoetan eragileak konbinatzen direnean, ukatzailea ebaluatzen da lehen, ondoren, eta ordena zainduz, konjuntzio eragilea eta batuketa logiko familiako disjuntzioekin amaitzeko. Horregatik ondoko programan ez da parentesirik behar:
PROGRAM BolearrenLehentasuna ; VAR Eragigai1, Eragigai2 : Boolean ; BEGIN Eragigai1 := FALSE ; Eragigai2 := TRUE ; WriteLn (‘NOT Eragigai1 OR Eragigai2 = ‘, NOT Eragigai1 OR Eragigai2) ; WriteLn (‘Eragigai1 OR NOT Eragigai2 = ‘, Eragigai1 OR NOT Eragigai2) ; END.
Parentesiak soberan egon arren, argitasunagatik ipintzea komeniko litzateke programa errazago irakurri ahal izateko horrela idatziz: Eragigai1 OR (NOT Eragigai2). BolearrenLehentasuna izeneko programa baliatuz aldaketak egin eta emaitzak interpretatu.
Zenbaitetan kalkulu logikoak zuzentasunez burutzeko parentesiak derrigorrezkoak dira. Adibidez, ondoko proposizioekin kalkulu logiko bat egin nahi da:
Proposizio horiek egia direnean, dagozkien aldagaietan TRUE gordeko dugu, eta gezurra direnean berriz FALSE. Egun jakin batean, hiru aldagaien balioak ezagunak direlarik zer nolako plana izango dugun ondoko adierazpen logikoaren bitartez kalkula daiteke (plan ona denean adierazpenak TRUE balio du, eta kontrakoan espresioaeren balioa FALSE izango da).
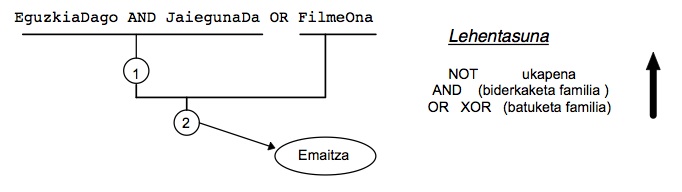
Egun eguzkitsua bada kanpora irten gaitezke (eginkizun hori plan on bat dela kontsidera dezakegu) baina horretarako lanera ez joatea ezinbestekoa denez, proposizio biak konjuntzioz lotuko ditugu. Baina bada beste posibilitate bat eguna galdutzat ez jotzeko, pelikula on bat ikustea alegia; eta hori egiteko gaba edo arratsaldea aprobetxa dezakegunez ez dago jaia izatearen baldintzarik.
Baina parentesiak jarriz, interpretazioa erabat aldatzen da: EguzkiaDago AND (JaiegunaDa OR FilmeOna)
Plan ona izateko derrigorrez egun eguzkitsua behar da, eta gainera bi egoera hauetatik bat egia izango da (edo biak): jaieguna izatea, filme ona programaturik egotea.
Egoerak subjetiboak direnez eta norberaren gogoarekin zerikusia dutenez, espresio logiko biak egokiak izan daitezke baina bakoitzak pentsakera desberdina isladatzen du. Arau orokor bezala, eragileen lehentasun arauen arabera soberan egon arren, irakurketa erraztuko luketen parentesiak erabiltzea gomendatzen da. Jarraian ematen den programa azter ezazu:
PROGRAM UrtebetetzeaAsmatu ; CONST NIRE_HILA = 3 ; NIRE_EGUNA = 26 ; VAR Eguna, Hila : Byte ; BEGIN Write (‘Egun bat sartu: ‘) ; ReadLn (Eguna) ; Write (‘Hilabete bat sartu: ‘) ; ReadLn (Hila) ; Write (Hila, ‘/‘ ,Eguna) ; WriteLn (‘ nire urtebetetzea: ‘, (Eguna=NIRE_EGUNA) AND (Hila=NIRE_HILA)) ; END.
UrtebetetzeaAsmatu programa honen ezaugarria erabiltzareari datuak eskatzen dizkiola eta horiek landu ondoren informazio bat erantzuten duela, orain artekoak ez bezala elkarreragilea da. Programa honetan lehenengo aldiz ReadLn agindua agertzen zaigu, aurrerago ikasiko dugu baina orain aldagai bati teklatuaren bitartez balioren bat emateko dela jakin dezagun; egun eta hilabete bat zehaztu ondoren emaitza lortzeko adierazpen boolear bat ebaluatu behar da:
Egun bat sartu: 26 Hilabete bat sartu: 12 12/26 nire urtebetetzea: FALSE _
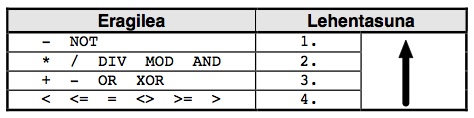
Orain arte aipatu ditugun eragileen lehentasuna jarraian laburbiltzen da:
Ez da ahaztu behar familien arteko lehentasuna aldatzeko parentesien bitartez egiten dela. Eta lehentasun bereko eragileak adierazpen batean aurkitzean, adierazpenean ezkerragora agertzen den eragiletik hasten da ebaluazioak egiten Turbo Pascal lengoaia.
Jarraian agertzen diren adierazpen logikoen balioa iruzkin bezala jarri da. Baldin eta x=12.4 , y=37.0 , z=0.1 eta ordenaturik=FALSE orduan:
|
| PARAMETRO IZATEAN JOKAMOLDEA Boolean datu-mota sinplea izanik azpiprograma batean honela agertuko da jokamoldearen arabera:
|
| ADIBIDEAK Hona hemen datu-mota boolearrak erabiltzen dituzten zenbait programa:
|
BOOLEAN datu-mota
Requisitos de finalización
BOOLEAN
Última modificación: jueves, 29 de agosto de 2013, 10:55