
Diseñar un controlador PD mediante la técnica del lugar de las raíces para un sistema que tiene la función de transferencia G(s)=1∕s2. Mediante el controlador se quiere que el sistema en lazo cerrado cumpla las siguientes especificaciones: tiempo de pico 3,14 seg. y tiempo de establecimiento 4 seg., siendo la realimentación unitaria. Analizar el comportamiento del sistema en lazo cerrado utilizando el controlador diseñado.
Solución:
Teniendo en cuenta las especificaciones y las expresiones T1=π∕ωd y Tp=4∕(δωn), se requiere que los polos dominantes sean (δ=0.707, ωn=1,414):

Para obtener el valor del parámetro Td del controlador PD se aplica la condición del argumento:

siendo el parámetro α, la fase que debe añadir el controlador PD para que el punto s1 pertenezca al lugar de las raíces. En este caso arg(s1)=3π/4 y, por tanto, α=π∕2. Por tanto, el parámetro Td queda:


Entonces, la función de transferencia en lazo abierto queda:

Está claro que la influencia del cero no es despreciable (tiene la misma abcisa que los polos en lazo cerrado escogidos). Hay que recordar que el diseño se ha realizado suponiendo el sistema de segundo orden típico sin ceros, y, como se ha estudiado en el capítulo 6 (Sist. de segundo orden con cero adicional), el cero adicional hace que el comportamiento sea más rápido (el tiempo de pico es menor, en este caso pasa de 3,14 seg. a 1,55 seg.) y con más rebose (pasa del 5% si no tuviera el cero al 20% teniéndolo).
Si se considera fija la constante derivativa Td se puede analizar la variación en el comportamiento del sistema en lazo cerrado si varía la constante proporcional. Para ello vamos a construir el Lugar de las Raíces (se aplican las reglas de construcción a la función G(s), de la cual se excluye el 2 correspondiente a la ganancia del control PD calculado anteriormente):
- Dos ramas, una acaba en el cero de G(s) (es decir, en s=-1) y la otra, a través del eje real, en -∞ (una única asíntota).
- Ángulo de salida de los polos de G(s): planteando la condición del argumento para el polo (s=0)

Para n=0, el ángulo de
salida es α=- , para n=-1, el ángulo de salida es α=
, para n=-1, el ángulo de salida es α= .
.
- El ángulo de llegada al cero es evidente del comportamiento en el eje real.
- Posibles puntos de dispersión, soluciones de la ecuación

Así, el punto s=0 es punto de dispersión y s=-2 es un punto de encuentro.
- Aplicando el Criterio de Routh-Hurwitz a la ecuación característica del lazo cerrado, s2+Ks+K=0 para K>0, se puede estudiar la estabilidad y los cruces del eje imaginario. Tabla de Routh:

Por tanto, si K>0 el sistema es estable en lazo cerrado. Con esta información el Lugar de las Raíces viene dado por la siguiente figura:
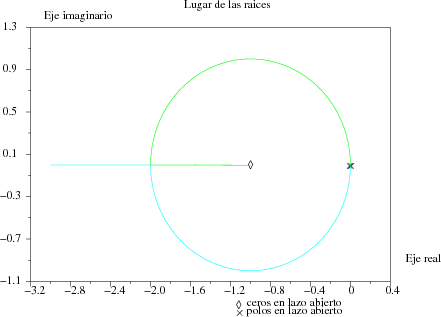
Se puede observar que partiendo de K=0, al aumentar la ganancia proporcional K:
Casi todo el análisis anterior se ha realizado obviando el cero en lazo cerrado s=-1 (introducido por el controlador PD), que magnifica algunas de las características (rebose), disminuye otras (tiempo de pico, de respuesta y de retardo) y modifica otras (tiempo de establecimiento). En este contexto, para valores muy grandes de K el polo que se va acercando al cero y el propio cero llegan a estar muy próximos con lo que sus efectos se compensan. En consecuencia, el sistema se comporta como uno de primer orden y con el polo muy alejado. Es decir, respuesta muy lenta y sin rebose ante entrada escalón.
Finalmente, se deja como ejercicio realizar el mismo análisis para variaciones de la constante derivativa Td, manteniendo fija la ganancia propocional K.