|
6.1 Introducción
6.2 Señales
de entrada tipo para el análisis transitorio de los
servosistemas
6.3 Especificaciones del transitorio
6.4 Estudio
de la respuesta transitoria
6.4.1 Sistemas de primer orden
6.4.2 Sistemas de primer orden con cero
adicional
6.4.3 Sistemas de segundo orden
6.4.4 Sistemas de segundo orden con ceros y polos
adicionales
6.4.4.1 Cero adicional
6.4.4.2
Polo adicional
6.4.5 Sistemas de orden superior
La forma más intuitiva y sencilla de estudiar los sistemas de control es en el dominio temporal, por lo que resulta interesante, en general, calcular sus respuestas temporales. De esta forma se puede tanto analizar el sistema como diseñarlo de forma que cumpla una serie de especificaciones de carácter temporal.
De manera general se puede decir que la respuesta temporal de un sistema dinámico a una excitación que posee ciertas propiedades a partir de un instante t0 (por ejemplo, una excitación periódica, o una que se mantenga en un valor constante a partir de t0, o que tenga una pendiente constante, etc...) consta de dos partes (Figura 6.1 ): la parte transitora yt(t), y la permanente o estacionaria yp(t), siendo la respuesta del sistema la suma de las dos:
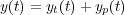
La parte transitoria se caracteriza porque su influencia en la respuesta del sistema disminuye con el tiempo, de modo que el limt→∞yt(t)=0, y representa el "acondicionamiento" del sistema hasta alcanzar su régimen estacionario impuesto por la constancia en la excitación. Puesto que inercia y rozamiento son factores característicos de todo servomecanismo (aparte de otros factores de retardo que puedan existir) es claro que la salida del sistema no seguirá inmediatamente a variaciones súbitas de la entrada, por lo que aparecerá siempre un régimen transitorio. En la mayoría de los casos prácticos la respuesta transitoria presentará oscilaciones amortiguadas antes de alcanzar un estado de equilibrio (régimen permanente).
El régimen permanente no está definido de manera normalizada. Por ejemplo, en el análisis de circuitos se suele definir como aquél régimen que es constante. En las aplicaciones de servosistemas, sin embargo, cuando una respuesta alcanza su régimen permanente puede continuar siendo todavía una función del tiempo. En sistemas de control podemos definir la respuesta en régimen permanente como la respuesta cuando el tiempo tiende a infinito. Si la respuesta en régimen permanente no coincide exactamente con la entrada decimos que el sistema presenta un error estacionario, indicándonos la precisión del sistema. El régimen permanente será tratado en profundidad en el capítulo 8.
Las especificaciones temporales de diseño para sistemas de control son las características que el diseñador desea que tenga la respuesta temporal del sistema. Dichas especificaciones incluyen normalmente varios valores que determinan la respuesta en el tiempo deseada para una entrada especifica así como una exactitud deseada en estado estacionario. Sin embargo, rara vez se puede llegar a un fiel cumplimiento de todas las especificaciones siendo preciso adoptar una decisión de compromiso, es decir, sacrificar el cumplimiento de una o varias especificaciones para que otras se satisfagan exactamente o encontrar una solución de control que sea la más próxima a la ideal aunque no satisfaga exactamente alguna de las especificaciones requeridas. En cualquier caso, la decisión a adoptar dependerá del tipo de tarea a controlar. En este sentido, hay que tener en cuenta que es muy distinto, por ejemplo, diseñar un sistema de control para regular la temperatura de una habitación que para regular la temperatura de un reactor nuclear.
El diseño de un servosistema no se suele realizar de acuerdo a su correcto comportamiento para una señal de entrada determinada ya que, generalmente, ésta no es conocida de antemano. Por ejemplo, en un radar de persecución la posición y velocidad del blanco pueden variar de modo imprevisible de forma que no puede expresarse analíticamente la señal de entrada al sistema por una simple ecuación.
La forma habitual de actuar, tanto en el diseño como en el análisis, es considerar la respuesta del sistema con arreglo a un grupo de excitaciones estándar y juzgar la calidad del sistema de una forma más o menos semiempírica. De estas experiencias se obtienen ciertas características del sistema que nos servirán para definir de alguna forma su comportamiento y con ello predecir la respuesta del mismo cuando la entrada sea otra cualquiera. Este método de estudio es bastante útil pues hay una correlación razonable entre la respuesta del sistema a una entrada estándar y la respuesta actuando en condiciones normales.
Teniendo en cuenta lo anterior, se puede analizar un sistema de dos formas diferentes atendiendo al tipo de señal que se use para excitarlo:
Naturalmente, las características de las respuestas de un mismo sistema obtenidas según uno u otro método deben de guardar ciertas relaciones, y del estudio de una de ellas se pueden inferir resultados para la otra. En esta asignatura se va a realizar el análisis de los sistemas de control en el dominio temporal.
En la Figura 6.2 se muestran las señales patrón o estándar más comúnmente utilizadas en el estudio temporal:
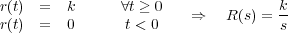
La función escalón unitaria (k = 1) sirve como excitación estándar en un primer análisis del transitorio de todo servosistema. Dado que la información que de su aplicación se obtiene es en muchos casos suficiente para inferir de una forma aproximada el comportamiento del sistema ante cualquier otra entrada, va a ser la señal de excitación que más se va a utilizar a lo largo de toda la asignatura.
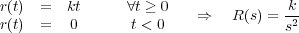
En algunos casos, el estudio de la respuesta del sistema ante una señal de entrada de este tipo es fundamental para obtener información que complete a la obtenida mediante el análisis ante entrada escalón.
Entrada parabólica: Es el cambio gradual de la velocidad de crecimiento del valor de la variable de entrada. Su representación matemática es:
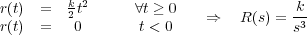
Como se ha explicado anteriormente, en general, para analizar el comportamiento transitorio de la respuesta de un sistema se utiliza como entrada la función escalón unitario. Sobre bases totalmente empíricas y basadas en la experiencia, se acostumbra a caracterizar la respuesta transitoria de un servomecanismo mediante una serie de parámetros de tal forma que con el conocimiento de los valores de todos o al menos de varios de dichos parámetros es posible predecir, de una forma más o menos aproximada, la dinámica del sistema aún cuando la entrada sea otra diferente.
Si se considera que la respuesta de un gran número de sistemas ante entrada escalón unitario tiene la forma de la Figura 6.3 (notad que la salida está dividida por la ganancia K del sistema), se puede decir que los parámetros o especificaciones que caracterizan la parte transitoria de la salida de dicho sistema son:
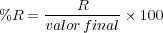
Esta especificación es una medida de la estabilidad relativa del sistema.
Una vez definidos los parámetros que caracterizan la respuesta transitoria de un sistema se puede concluir que los problemas de diseño y análisis de los sistemas de control son dos enfoques del mismo problema. Así, si se miden los parámetros definidos arriba en la respuesta transitoria de un sistema de control, su estudio permite conocer el comportamiento del servosistema en lo que se refiere a la presencia de retardos, rapidez, amortiguación, estabilidad, etc., pudiendo así juzgar si dicho sistema resulta eficaz para la tarea que ha sido diseñado, o por el contrario, si se hace necesaria una modificación de alguna de sus características. Se trata en definitiva de un problema de análisis.
Por otro lado, si se dispone de un sistema de control en el que se hace necesaria la modificación de alguna de sus características mediante la introducción de un dispositivo adicional, como puede ser un controlador, un sensor, un actuador, etc., entonces el problema consiste en elegir la respuesta deseada del sistema ante la señal de referencia, o lo que es lo mismo, especificar la curva de salida. Esta elección se realiza seleccionando las especificaciones adecuadas (rebose, tiempo de retardo, subida o establecimiento máximos, etc.), y calculando el elemento ajustable adecuado (normalmente el controlador). Se trata en este caso de un problema de diseño.
Estudiando detenidamente ambos casos se observa que se tratan del mismo problema, pero siguiendo enfoques distintos.
Un sistema de primer orden es aquel en el que la mayor derivada de la señal de salida en la ecuación diferencial que relaciona sus señales de entrada y salida es de orden uno, esto es, su función de transferencia solo tiene un polo.
Teniendo en cuenta el principio de causalidad un sistema de primer orden puede tener un cero como máximo. En un primer estudio se considera el caso en el que la función de transferencia es de la forma:
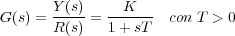
dejando para el siguiente punto el caso de un sistema de primer orden con cero adicional.
A la hora de analizar el transitorio de este sistema se va a calcular la expresión analítica de su señal de salida ante la entrada escalón unitario. Para una mayor profundización en el conocimiento del comportamiento del sistema podría ser de utilidad el realizar el mismo estudio para otra señal de entrada, como puede ser la rampa o la parábola, o una combinación de ellas. Sin embargo, como ya se explicó en la Sección 6.2, en general basta con analizar el comportamiento de un sistema ante entrada escalón unitario para inferir su respuesta ante otro tipo de entradas.
Para una entrada escalón unitario se tiene que la salida es:
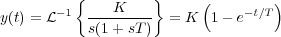
Como se puede observar estudiando la señal de respuesta del sistema de primer orden, dada la simplicidad del mismo no es necesario el cálculo de los diferentes parámetros o especificaciones que definen el transitorio de la señal. La respuesta del sistema queda completamente definida con la ganancia del sistema K, y con la constante de tiempo T que se define como el tiempo que tarda el sistema en alcanzar el 63,21% del valor final de la señal de salida (Figura 6.4). La respuesta del transitorio está desprovista de oscilaciones, y por ello no tiene sentido ni el rebose ni el tiempo de pico.
Dado que a lo largo de esta asignatura se van a analizar y diseñar los sistemas de control en el plano s, es conveniente que se llegue a tener facilidad en relacionar la situación de los polos y ceros de la función de transferencia de un sistema con su comportamiento ante las diferentes entradas patrón, y en concreto ante la entrada escalón.
En el caso del sistema de primer orden se observa que cuanto mayor sea la constante de tiempo T más lentos son tanto la velocidad de respuesta como la llegada al estado estacionario (en estos sistemas estas dos características están siempre relacionadas, no así en general), y viceversa. Y dado que el polo está situado en s = -1∕T, se puede concluir que cuanto más cerca esté el polo del eje imaginario (menor sea su módulo) más lento será el sistema (Figura 6.5), siendo esta característica general para todos los sistemas, cualquiera que sea su orden.
Si a un sistema típico de primer orden se le añade un cero se obtiene un sistema con exceso polo-cero nulo de la forma:

Se puede observar que si el sistema es estable el valor final de la salida del sistema ante entrada escalón unitario es:

Es decir, el mismo valor que el de un sistema de primer orden sin cero adicional (observad la forma de escribir el numerador). Sin embargo, si mediante el teorema del valor inicial se obtiene el valor de la señal de salida en el instante cero (t=0+):

|
En la Figura 6.6
se observa que si a>T la salida tenderá
asintóticamente al valor final “por arriba”, desde el valor inicial
y(0+)= , y si a<T lo
hará “desde abajo”. Notad que la presencia del cero adicional introduce
una discontinuidad en la señal de salida en el instante t=0, ya que, en
general, y(0-), que es la salida del sistema justo antes de
aplicarse la señal de entrada (puede ser nula si el sistema está en
reposo), e y(0+)=
, y si a<T lo
hará “desde abajo”. Notad que la presencia del cero adicional introduce
una discontinuidad en la señal de salida en el instante t=0, ya que, en
general, y(0-), que es la salida del sistema justo antes de
aplicarse la señal de entrada (puede ser nula si el sistema está en
reposo), e y(0+)= , que es el valor de la salida en el instante
inmediatamente posterior al momento en que se aplica la entrada escalón
unitario (instante en que la señal de entrada pasa del valor 0 al 1),
son valores distintos. En definitiva, la discontinuidad de la señal de
entrada se transmite a la señal de salida del sistema. Esto no ocurre
en los sistemas de primer orden sin cero adicional (Figura 6.4).
, que es el valor de la salida en el instante
inmediatamente posterior al momento en que se aplica la entrada escalón
unitario (instante en que la señal de entrada pasa del valor 0 al 1),
son valores distintos. En definitiva, la discontinuidad de la señal de
entrada se transmite a la señal de salida del sistema. Esto no ocurre
en los sistemas de primer orden sin cero adicional (Figura 6.4).
Un sistema de segundo orden es aquel cuya función de transferencia tiene dos polos. Al igual que en los sistemas de primer orden, en cualquier sistema físico real el número de ceros debe ser inferior o a lo sumo igual al de polos, y por ello los sistemas de segundo orden pueden tener como máximo dos ceros.
En general, y debido a su simplicidad, se tiende a intentar modelar cualquier sistema como uno de segundo orden, por lo que es necesario estudiar en profundidad dicho tipo de sistemas. Así, en un principio se van a estudiar los sistemas de segundo orden sin ningún cero para más adelante estudiar el efecto de añadirle ceros o polos obteniendo sistemas de orden superior y/o con ceros.
Si se considera, entonces, el caso de un sistema de control de segundo orden sin ceros, se puede siempre reescribir su función de transferencia para que quede de la forma:
 |
(6.1) |
donde K es la ganancia del sistema (ganancia a baja frecuencia o ante entrada escalón), δ el coeficiente de amortiguamiento, y ωn la frecuencia natural o propia del sistema (ωn>0). En definitiva, se puede caracterizar este tipo de sistemas por estos tres parámetros, a los cuales se dará un sentido físico más adelante.
Para analizar la dinámica del sistema es necesario estudiar la situación de sus polos para los diferentes valores de los parámetros, o lo que es lo mismo, obtener una relación entre éstos, la situación de los polos en el plano s, y el comportamiento del sistema ante las entradas patrón. Los dos polos del sistema son las raíces de la ecuación característica del sistema (ecuación resultante de igualar a cero el denominador de la función de transferencia), que para el sistema (6.1) son:

Como se
puede observar, la situación de los polos no depende de la ganancia
K, la frecuencia natural ωn
influye directamente en el módulo de los polos
(su distancia con respecto al origen del plano s), y finalmente, del
coeficiente de amortiguamiento δ depende
que los polos sean reales (si  ≥1) o complejos conjugados (si
≥1) o complejos conjugados (si  <1).
<1).
Dada la importancia del parámetro δ, se va a analizar en detalle la evolución de los polos según varie el coeficiente de amortiguamiento:

Corresponde a un sistema críticamente estable, esto es, que ante entrada escalón presenta una salida oscilatoria mantenida sin amortiguamiento (no decae a un valor finito).

Se trata, en este caso, de un sistema estable con salida oscilacitorio ante una entrada constante (escalón). Las oscilación se va amortiguando hasta que desaparece alcanzandose un valor constante en la salida.

Se trata de un sistema estable que ante entrada constante no presenta oscilaciones al igual que los sistemas de primer orden, y se puede comprobar, que a diferencia de éstos, la respuesta del mismo ante entrada escalón presenta pendiente nula en el instante inicial.
El radicando es positivo (δ2-1>0), por lo que las raíces son reales y distintas. Se puede demostrar que son ambas negativas, y que por lo tanto el sistema es estable y no presenta oscilaciones ante entrada constante.
Teniendo en cuenta todo lo anterior se deduce fácilmente que si se mantiene la frecuencia natural ωn constante, y se varía el coeficiente de amortiguamiento δ de 0 a ∞, entonces las raíces de la ecuación característica describen la gráfica de la Figura 6.7.
En este apartado se va a estudiar en detalle el caso conocido como subamortiguado (δ<1) dado que gran cantidad de sistemas que ante entrada constante presentan oscilaciones en su respuesta pueden aproximarse por sistemas de segundo orden subamortiguados con una exactitud aceptable. Para ello se va a analizar la relación existente entre la situación de su pareja de polos complejos conjugados en el plano s con el comportamiento transitorio de dicho sistema.
Entonces para el caso en el que el coeficiente de amortiguamiento es inferior a la unidad (δ<1) la situación de los polos complejos conjugados se puede representar gráficamente según el diagrama de la Figura 6.8 .
|
Se puede comprobar fácilmente que la representación cartesiana utilizada hasta el momento para situar los polos puede sustituirse por una representación polar modificada, para simplificar los cálculos, de la forma:

Se puede observar que en definitiva el módulo de los polos complejos conjugados es la frecuencia natural (ωn), y el ángulo que forma la recta que une uno cualquiera de los polos con el eje real negativo depende únicamente del coeficiente de amortiguamiento (δ).
El estudio analítico de la situación de los polos de un sistema de segundo orden aquí realizado servirá más adelante para relacionar la respuesta transitoria de un sistema de control y la localización de las raíces de su ecuación característica o polos de su función de transferencia. Este estudio se ha realizado ante entrada escalón, aunque por extensión se podrían deducir conclusiones válidas para cualquier otra entrada.
A continuación se va a proceder a obtener analíticamente las especificaciones que permiten caracterizar el transitorio de un sistema de control en función de los parámetros del sistema de segundo orden, o lo que es lo mismo, de la localización de sus polos.
La transformada de Laplace de la señal de salida del sistema de control de segundo orden estudiado (6.1) es:

Si se aplica una entrada escalón unitario (R(s)=1∕s) la respuesta temporal del sistema es:

En el caso que se quiere estudiar (0≤δ<1), se obtiene:
![[ - δωnt ( ∘ ------ √-----2)] y(t) = K 1 - e√------sen ωn 1- δ2t+ arctan-1---δ- 1- δ2 δ](/file.php/83/cap6_html/capitulo630x.png) |
(6.2) |
donde se tiene una respuesta con oscilaciones, que es la respuesta temporal típica de un sistema de segundo orden con polos complejos conjugados.
En (6.2) se distinguen claramente la parte transitoria de la respuesta del sistema (segundo término) que tiende a cero cuando t →∞, y la parte permanente (primer término).
También se puede observar que la frecuencia a la que oscila la respuesta del sistema o frecuencia amortiguada o de oscilación transitoria varía con el amortiguamiento δ:

Analizando este expresión se deduce fácilmente que la frecuencia natural del sistema ωn es la frecuencia a la que oscilaría la respuesta del sistema en el caso de que el amortiguamiento fuese nulo (δ=0).
En la Figura 6.9 se representan algunas curvas de respuesta para diferentes valores de δ en función del tiempo normalizado ωnt.
|
Observando esta figura se corrobora el estudio que se ha hecho anteriormente sobre la forma de la señal de salida en función del coeficiente de amortiguamiento. Se puede precisar aún más y añadir una serie de conclusiones que permitirán analizar detalladamente los sistemas de segundo orden:
Una vez estudiado el comportamiento del sistema en función del valor del coeficiente de amortiguamiento se puede entender el sentido físico del mismo, que no es otro que reflejar el grado de amortiguamiento de la señal de respuesta temporal del sistema ante entrada constante.
A partir de la expresión de la señal de salida del sistema ante entrada escalón (6.2) se pueden hallar las expresiones para las diferentes especificaciones que definen el transitorio de un sistema.

que permite obtener los instantes de tiempo en los que la curva de respuesta presenta pendiente nula (máximos y mínimos):
 |
(6.3) |
Sustituyendo el tiempo de pico en la respuesta del sistema (6.2) se puede obtener el rebose de la misma:
 |
(6.4) |
y el rebose porcentual:
 |
(6.5) |
observándose que este último únicamente depende del coeficiente de amortiguamiento.
|
En la Figura 6.10 se muestra el rebose R y el tiempo de pico normalizado ωnT1 en función del coeficiente de amortiguamiento δ. Se observa que a la hora de diseñar un sistema de control es necesario un compromiso entre el rebose y el tiempo de pico que se deseen para el mismo, dado que al mejorar uno de ellos se empeora el otro. Esto es, si se desea un sistema muy rápido en respuesta será a costa de empeorar su transitorio (aumentar el rebose).
 |
(6.6) |
Se observa que, como es lógico, al igual que el tiempo de pico el tiempo de subida es inversamente proporcional a la frecuencia de oscilación transitoria (o la parte imaginaria de los polos complejos conjugados de la función de transferencia).
 |
(6.7) |
Y para aquellos sistemas donde 0,9<δ<1,4 se puede utilizar otra aproximación:

Se ha podido observar que para los casos que se puede representar un sistema con una función de transferencia de segundo orden sin ceros, las especificaciones que definen su transitorio ante entrada escalón unitario, y por extensión su comportamiento general, son de muy fácil manejo y tratamiento matemático. Así, tanto si se trata de un problema de análisis como de diseño, puede en muchos casos preferirse una pérdida de exactitud si el sistema no es exactamente de segundo orden sin ceros para que el cálculo sea sencillo, que optar por una representación más precisa (orden superior o adición de ceros) y complicar en exceso el tratamiento matemático como se verá en apartados posteriores.
Hasta ahora únicamente se han estudiado los sistemas de segundo orden con numerador constante. En este apartado se calcularán los parámetros típicos que caracterizan la respuesta transitoria de un sistema de segundo orden cuando el numerador presente un cero, o cuando el sistema tiene otro polo (sistema de tercer orden), y se establecerán unas relaciones con el sistema sin cero, o sin polo adicional. En definitiva, se llegará a establecer la influencia de un cero y de un polo en un sistema de control.
|
Para facilitar los cálculos y tener una visión más general de la influencia de polos y ceros, se utilizarán para fijar la posición de la pareja de los polos complejos conjugados del sistema de segundo orden, el cero y el polo adicional los ángulos θ, θc y θp, respectivamente, tal como se ve en la Figura 6.11 .
Tal como se calculó en la sección 6.4.3 la respuesta temporal de un sistema de segundo orden sin ceros ante entrada escalón escalón unitario es:
 |
(6.8) |
Se ha considerado en este caso que el sistema tiene ganancia unitaria (K = 1).
Con vistas a simplificar cálculos se van a tener en cuenta las siguientes relaciones:

Así la expresión (6.8) queda:

Realizando los cambios correspondientes se obtienen las expresiones de los diferentes parámetros del transitorio del sistema de segundo orden calculados en la sección 6.4.3 :
 |
(6.9) |
 |
(6.10) |
 |
(6.11) |
 |
(6.12) |
Si al sistema típico de segundo orden subamortiguado se le añade un cero en s=-1∕a con a>0 (la configuración de polos y ceros se ve en la Figura 6.12), su función de transferencia quedará:

Se puede calcular la respuesta a una entrada escalón unitario de este sistema:
 |
(6.13) |
A continuación se va a proceder a calcular las expresiones de las diferentes especificaciones y comparar con las del sistema sin el cero adicional.

y por tanto el tiempo de subida será:

Derivando e igualando a cero la respuesta del sistema (6.13) se obtienen sus máximos:

y por tanto el tiempo de pico es:

Que confirma, lógicamente, lo dicho para el tiempo de subida, ya que tanto Ts como T1 son parámetros que miden la velocidad de respuesta del sistema.
Se obtendrá igual que en el caso sin cero, restando la unidad a la respuesta e igualando la envolvente superior al valor 0,02 (2%):

En la Figura 6.13 se muestra la variación del tiempo de establecimiento normalizado δωnTp en función del angulo θc, tomando el valor de θ como parámetro.
|
Se observa que cuanto
más cerca esté el par de polos complejos conjugados del eje imaginario
(θ→90o) la
existencia de un cero adicional aumenta el tiempo de establecimiento de
una forma perceptible cuando el cero está muy cerca de los polos. Por
el contrario si los polos no están muy cerca del eje imaginario existe
un punto en el que el tiempo de establecimiento es mínimo.
Se puede observar que cuando el cero adicional está muy alejado del
eje imaginario (θc pequeño) el tiempo de establecimiento es
el del sistema de segundo orden típico.
Sustituyendo el valor del tiempo de pico (T1) en la respuesta transitoria (6.13) y restándole la unidad (dado que el sistema estudiado es de ganancia unitaria) se obtiene el valor de la sobreoscilación:

En la Figura 6.14 se representa el rebose (R) en función del ángulo θc, tomando θ como parámetro. Se observa que el rebose aumenta (para un valor dado de θ) al aumentar θc, esto es, al acercarse el cero adicional al eje imaginario. De igual forma se observa que al aumentar θ (para un valor de θc) aumenta el rebose (igual que en un sistema típico de segundo orden) y, como en las otras especificaciones, para el caso del cero adicional muy alejado del eje imaginario el rebose corresponde al del sistema de segundo orden típico.
Como conclusión final cabe decir que la adición de un cero al sistema típico de segundo orden hace más rápido y oscilatorio al sistema, y tanto más cuanto más se aproxima la posición del cero al eje imaginario. Por el contrario, si el cero está alejado del eje imaginario su influencia es pequeña, y tanto más pequeña cuanto más alejado esté. Se puede decir que esta conclusión es general y, por tanto, sea cual sea el orden del sistema si se le añade un cero el efecto es el mismo.
Como comentario final decir que la sola adición de un cero a la función de transferencia de segundo orden ha complicado los cálculos de una forma apreciable, que aún se complicará mucho más en el caso siguiente.
Si a un sistema de segundo orden con polos complejos conjugados, sin ceros y ganancia unitaria (K=1) se le añade un polo la función de transferencia (Figura 6.15 ) quedará:
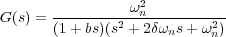 |
(6.14) |
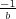 , con lo que, en realidad, el sistema pasa a
ser de tercer orden.
, con lo que, en realidad, el sistema pasa a
ser de tercer orden.La respuesta ante una entrada escalón unitario (caso 0≤δ<1) será:
![e-ωdtcotgθ[ -ωdtcotgθp 2 ] y(t) = 1- --sen2θ-- sen(ωdt +θ - θp)sen (θ + θp)+ e sen θp](/ensenanzas-tecnicas/automatica/cap6_html/capitulo663x.png) |
(6.15) |
Esta señal de salida puede dar lugar a tres tipos diferentes de respuesta según sea la situación del polo adicional respecto al par de polos complejos conjugados del sistema de segundo orden. Para llegar a esta conclusión se puede considerar al sistema (6.14) como si estuviese formado por un subsistema de primer orden y por otro de segundo orden situados en cascada. Es decir:
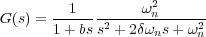
De esta forma si el valor de b (constante de tiempo del subsistema de primer orden) es muy pequeña comparada con la constante de tiempo del subsistema de segundo orden (1∕b≫δωn) se podría considerar que la respuesta del subsistema de primer orden es inmediata comparada con la del de segundo orden y, por lo tanto, la función de transferencia del primero se puede aproximar a la unidad, quedando el sistema total como uno de segundo orden típico. Hay que notar que el hecho de que 1∕b≫δωn supone que el polo adicional está muy alejado del eje imaginario en comparación con los polos complejos conjugados. Si suponemos a priori que el efecto es el mismo que con los ceros adicionales, entonces cuanto más alejado esté del eje imaginario un polo menor será su influencia en el transitorio del sistema. Por el contrario, si 1∕b≪δωn (polo adicional muy próximo al eje imaginario) la respuesta se aproximará a la del sistema de primer orden (sin oscilaciones y sin sobrepasar la unidad).
Finalmente, existe la posibilidad de que tanto 1∕b como δωn sean del mismo orden. En este caso la respuesta del sistema presentará oscilaciones inicialmente de valor inferior al final, pudiendo en máximos posteriores llegar a sobrepasar el mencionado valor. En las Figuras 6.16 se ha representado la respuesta de un sistema de tercer orden para valores fijos de ωn y θ, en función del ángulo θp, esto es, de la distancia del tercer polo a la pareja de polos complejos conjugados.
|
Como en casos anteriores se va a proceder a obtener las expresiones de las especificaciones que definen el transitorio de la señal de salida.
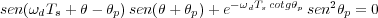
Se ha visto en la Figura
6.16 que si θp>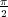 el sistema se parece a uno de primer orden,
con lo que la señal de salida únicamente alcanza el valor final en el
infinito, y por lo tanto no tiene sentido físico hablar de tiempo de
subida en este caso. En consecuencia, sólo interesa estudiar los dos
primeros casos en los que la respuesta alcanza el valor final varias
veces.
el sistema se parece a uno de primer orden,
con lo que la señal de salida únicamente alcanza el valor final en el
infinito, y por lo tanto no tiene sentido físico hablar de tiempo de
subida en este caso. En consecuencia, sólo interesa estudiar los dos
primeros casos en los que la respuesta alcanza el valor final varias
veces.
Se puede ver que si θp=0 (sin polo adicional) entonces Ts=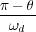 como ya se vio (6.9).
como ya se vio (6.9).
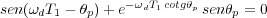 |
(6.16) |
Para θp>π∕2 no existen máximos, así que solo interesa el estudio para valores θp<π∕2. En la Figura 6.18 se representa el tiempo de pico normalizado (ωdT1) en función del ángulo θp (para θp<π∕2).
Se puede observar que según se acerca el polo adicional al par de polos complejos conjugados (crece θp), el sistema se hace más lento, esto es, aumenta el tiempo de pico, característica que ya se había visto con el tiempo de subida.
|
De la gráfica podemos deducir que para sistemas con parejas de polos complejos conjugados cerca del eje imaginario (θ grande) se consigue disminuir (hasta un valor mínimo) el tiempo de establecimiento. Por el contrario, si la pareja de polos no está cerca del eje imaginario acercar el polo adicional supone siempre un aumento del tiempo de establecimiento.
Utilizando la expresión obtenida para el tiempo de pico (6.16) y la respuesta del sistema (6.15) se obtiene:
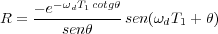
En la Figura 6.20 se puede observar, como ya se dijo anteriormente, que para ciertos valores de los ángulos θ y θp no existe rebose en la respuesta del sistema, por ejemplo, para los casos donde θ=80o y θp=85o.
Como conclusión puede decirse que la adición de un polo a un sistema típico de segundo orden, en el caso más interesante (1∕b>δωn, θp<π∕2), aumenta los tiempos de subida y de pico, a la vez que hace disminuir el rebose. Por tanto, si a un sistema se le añade un polo, éste ejerce una acción estabilizadora, haciendo el sistema más lento en respuesta.
Por último, corroborar lo dicho en el apartado anterior en el sentido de que cualquier aumento tanto en el grado de la función de transferencia de un sistema como en la adición de ceros complica los cálculos enormemente, teniendo por tanto el diseñador que decidir entre la exactitud y la manejabilidad en el diseño de sistemas de control.
Cuando se dispone de un sistema de control cuya representación matemática en forma de ecuación diferencial o de función de transferencia es de orden superior al segundo, con el fin de analizar su dinámica o de diseñar un controlador para el mismo es necesario simplificar el orden para que sea susceptible de manejarse fácilmente y, como se ha visto con los sistema de orden 1 o 2, de obtener expresiones matemáticas sencillas para las especificaciones del transitorio.
Si el sistema de la Figura 6.21 tiene la función de transferencia de orden n siguiente:
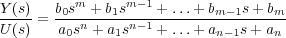
para determinar la respuesta transitoria de este sistema ante cualquier entrada es necesario descomponer en factores el polinomio denominador:
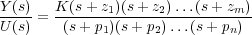
Considerando una entrada escalón unitario puede descomponerse en fracciones simples la transformada de Laplace de la señal de salida del sistema de la siguiente forma (vamos a suponer por simplicidad que todos los polos son reales y distintos entre sí):
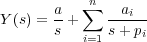
donde ai es el residuo del polo en s=-pi. Entonces, la señal de salida del sistema es:
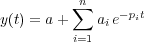 |
(6.17) |
Si todos los polos del sistema quedan en el semiplano izquierdo del plano s, la magnitud de los residuos determina la importancia relativa de cada sumando que compone la respuesta del sistema Y(s). Por lo tanto si el residuo es pequeño la contribución en la señal de salida de ese polo será también pequeña y se podrá eliminar el polo correspondiente disminuyendo de esta forma el orden del sistema. Existen dos causas que hacen pequeño el residuo de un polo:
De este modo, sistemas de orden alto pueden aproximarse por sistemas de orden más bajo, simplificándose notablemente su análisis. De todas formas, no siempre es posible simplificar un sistema hasta llegar a uno de segundo orden sin ceros.
Además, se puede decir que si un cero está muy alejado del eje imaginario tiene poca influencia en el transitorio del sistema y se puede eliminar sin pérdida grande de exactitud.
Resumiendo, y extendiendo ya el estudio a sistemas tanto con polos reales como complejos conjugados, los polos más cercanos al eje imaginario son los que marcan la dinámica del transitorio. Por ello se les llama polos dominantes. En la práctica se consideran dominantes cuando la relación de las partes reales con otros polos es inferior a una quinta parte, siempre y cuando no haya ceros en las proximidades.
Por último, teniendo en cuenta lo estudiado en la sección 6.4.2 (sistema de primer orden con cero adicional) habrá que tener cuidado cuando al eliminar ceros o polos con poca influencia en el transitorio de lugar a sistemas con exceso polo-cero nulo, ya que esto implica que la salida en el instante inicial no es nula (y(0+)≠ 0). Por lo tanto, si al eliminar un polo alejado se pasa de exceso polo-cero uno a cero los primeros instantes de tiempo la señal de salida del sistema original será muy diferente a la del sistema reducido (Figura 6.22).