|
Se presenta un procedimiento o algoritmo que resume todo el proceso de diseño de un sistema de control en el que estará incluido el proceso de modelización del sistema a controlar, su análisis, elección de elementos accesorios al mismo y finalmente el diseño del controlador adecuado para el correcto funcionamiento del conjunto. Y finalmente se estudiarán en profundidad los controladores tipo PID y sus variantes.
10.1 Introducción
10.2 Procedimiento de resolución de un diseño de
control
10.3 Control PID
10.3.1 Acciones básicas de control
10.3.2 Sintonía de PIDs
10.3.2.1 Sintonía de Ziegler-Nichols
10.3.2.2 Sintonía en el Lugar de las Raíces
10.3.2.3 Sintonía manual
10.4 Modificaciones al control PID
En los capítulos anteriores se ha estudiado, primeramente, toda una serie de herramientas que permiten obtener las ecuaciones matemáticas que representan al sistema, esto es, obtener un modelo del mismo que refleje su comportamiento de la forma más exacta posible sin sacrificar con ello su manipulabilidad (ecuaciones diferenciales, funciones de transferencia, respuesta impulso y diagramas de bloques). En segundo lugar se han estudiado varias herramientas que han permitido analizar características del comportamiento de dichos sistemas como pueden ser la estabilidad, rapidez de respuesta, duración del transitorio, capacidad de seguir a la entrada, etc. (criterio de Routh-Hurwitz, lugar de las raíces y coeficientes estáticos de error).
Una vez analizado todo lo anterior sólo resta diseñar la parte que falta en el lazo de control para que el sistema se comporte de la forma deseada, esto es, diseñar el controlador que va a generar la señal de control que excite al sistema propiamente dicho.
Este paso ya se ha dado en varios ejemplos y problemas realizados hasta el momento, pero se hace necesario definir un procedimiento de resolución general del problema de diseño de un sistema de control, que se va a establecer en este capítulo.
La función de un controlador en un sistema de control automático es modificar el comportamiento del mismo, de modo que se ajuste a las especificaciones previamente fijadas en su diseño.
En la teoría clásica de control se considera el problema de diseño desde el punto de vista de conseguir que el sistema cumpla algunos valores deseados de ciertas especificaciones (rebose, tiempo de establecimiento, margen de fase, etc.).
En un sistema con compensación serie, cuyo esquema se muestra en la Figura 10.1, la misión del controlador cuya función de transferencia viene representada por Gc(s) será proporcionar una señal de control u(t) que excite al conjunto accionador-proceso que se esté controlando (Gp(s)), de tal forma que el sistema realimentado total cumpla las especificaciones pedidas en el diseño.
En general la función de transferencia del controlador tendrá la forma:
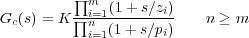
y el diseño del sistema de control consistirá en elegir adecuadamente la localización de los ceros (zi), polos (pi) y la ganancia (K) del controlador, de manera que se cumplan las especificaciones deseadas de estabilidad y precisión para la función de transferencia en lazo cerrado. La forma de elección de dichos parámetros dará lugar a diferentes métodos de diseño.
Estos métodos de diseño dan lugar a controladores complejos y específicos, siendo válidos únicamente para la aplicación desarrollada, y con dificultades añadidas para su ajuste o modificación en caso necesario, esto es, adolecen de una falta completa de uniformidad y versatilidad.
Para facilitar el diseño de sistemas de control de una gama lo más diversa posible, y optar por una sistemática de diseño más uniforme, en numerosas ocasiones se opta por la utilización de controladores normalizados con parámetros ajustables, que pueden ser utilizados en prácticamente cualquier sistema de regulación, sin más que permitir que sus parámetros puedan ajustarse dentro de un margen lo suficientemente grande de tal forma que regulen el proceso que se trate.
En este capítulo se van a estudiar sobre todo los controladores PID o casos particulares del mismo, y varios métodos de ajuste de sus parámetros.
Es de destacar la importancia que ha adquiriendo el control de procesos en la actualidad, ya que no se limita su utilización en procesos químicos o electrónicos, sino que se ha extendido a ramas de sociología y economía. En general en todos ellos existe una variable que se desea alcance un valor deseado con una rapidez determinada, o que no supere un cierto valor, y en definitiva se pueden aplicar las mismas herramientas que en los sistemas estudiados hasta el momento. El único problema para este tipo de sistemas es la enorme dificultad de obtener un modelo matemático fiable que represente al sistema real con una precisión adecuada.
El proceso de diseño de un sistema de control requiere una serie de pasos que van a permitir fijar las especificaciones deseadas para el sistema a controlar, elegir los elementos adecuados que sean necesarios para la construcción del sistema de control, y finalmente, diseñar el controlador adecuado.
Una característica principal de un verdadero proceso de diseño es que se trata de un trabajo integral en la que los diferentes pasos están interrelacionados, y es posible que se tenga que repetir alguno, rehacer trabajo ya realizado, o cambiar de estrategia.
A continuación se procede a enumerar las diferentes etapas del proceso de diseño (Figura 10.2 ):
Paso 1: Entender el proceso y traducir los requerimientos de comportamiento en especificaciones temporales, frecuenciales y de situación de polos y ceros.
En este paso se ha de entender exactamente el proceso, esto es, se ha de saber buscar unas ecuaciones que lo representen de una forma más o menos correcta, y si algo falla se deberá saber dónde puede haber estado el error, o dónde se ha tomado una simplificación que puede no ser correcta o se ha perdido demasiada exactitud con ella, etc.
|
En general se tienen una serie de requerimientos de comportamiento deseados para el sistema, como pueden ser el error permisible, la velocidad de respuesta deseada, el valor máximo de la señal de salida, etc.. Todos estos requerimientos habrá que traducirlos a especificaciones temporales, frecuenciales o de situación de polos y ceros que permitan su manipulación matemática (Figura 10.3).
Paso 2: Elección de sensores y actuadores.
En la elección de los sensores y actuadores será necesario tener en cuenta las variables físicas a medir o traducir, así como el rango de funcionamiento en el que van a evolucionar en situaciones normales.
También puede ser interesante, si se considera oportuno, medir perturbaciones, con lo que se deberá elegir un sensor adecuado para ello.
El actuador es el dispositivo que transforma la señal de control generada por el controlador en la señal que actúa sobre el sistema.
Los factores a tener en cuenta para la elección de un sensor o actuador son:
Tecnología: eléctrica, magnética, mecánica, etc.
Comportamiento funcional: linealidad, precisión, ruido, y para actuadores, potencia, máxima fuerza posible, etc.
Propiedades físicas: peso, tamaño, resistencia, etc.
Factores de calidad: mantenimiento, durabilidad, fiabilidad, etc.
Coste: gastos, mantenimiento, etc.
Paso 3: Desarrollo de un modelo lineal.
Una vez elegidos los sensores y actuadores necesarios, y analizando en profundidad el proceso, se hace necesario obtener un modelo matemático del sistema que sea exacto y manejable, esto es, modelo reducido y lineal del sistema real. En general los sistemas serán no lineales, y por ello habrá que elegir un punto de funcionamiento, y linealizar el sistema en ese punto obteniendo un modelo lineal que sea válido en un rango de funcionamiento lo mayor posible.
Siempre que sea necesario será conveniente validar el modelo con datos experimentales.
Paso 4: Diseño de controlador sencillo, del tipo PID o red de atraso-adelanto
Una vez dispuesto el modelo del conjunto que forman sistema, actuadores y sensores se traza el diagrama de Bode y/o el lugar de las raíces para hacerse una idea de la complejidad del sistema. Si el sistema en su totalidad es estable quizás lo más sencillo (si también es de fase mínima) sea trabajar con el diagrama de Bode. Si no lo es, lo mejor sería hacer el diseño en el lugar de las raíces.
De todas formas una práctica recomendable es intentar que las especificaciones deseadas para el sistema en lazo cerrado se cumplan con un controlador sencillo tipo PID o sus casos particulares, o del tipo atraso-adelanto (dos polos y dos ceros) incluyendo un control integral si se desea eliminar el error en régimen estacionario.
En este paso es posible encontrarse con problemas en el diseño que requieran una modificación del sensor o actuador escogido (Paso 2).
Por otra parte será necesario asegurarse que el controlador diseñado es físicamente realizable, y que la forma que toma la señal de control en el diseño realizado tome valores dentro del rango permitido para la misma.
Aunque se mencionan en algunos puntos de este capítulo, en esta asignatura no se ha estudiado la respuesta en frecuencia de un sistema lineal, ni las herramientas de análisis y diseño de sistemas de control mediante técnicas en frecuencia. Algunas de estas técnicas son la representación polar, el diagrama de Bode o de Nyquist, y el diseño de redes de compensación (redes de atraso, de adelanto y de atraso-adelanto) o de otros controladores (por ejemplo el PID y sus variantes) en el diagrama de Bode. Todas estas técnicas corresponderían a una asignatura continuación a la que nos ocupa.
Paso 5: Otros tipos de controladores
Si el diseño obtenido en el paso anterior no es todo lo satisfactorio que se desea, será necesario el uso de otro tipo de controladores más complejos como pueden ser: control óptimo, robusto, adaptativo, etc.
En caso de mejorar las prestaciones se cambia el controlador y se sigue adelante.
Paso 6: Simulación del control diseñado
Una vez realizado el diseño se deberá simular todo el sistema de control para asegurarse de que funciona correctamente.
En el modelo del sistema, sensores y actuadores es conveniente la introducción de todas las no linealidades y perturbaciones conocidas. De esta forma se puede asegurar que el sistema real funcionará de forma similar al simulado.
Paso 7: Construcción de un prototipo
Llegado a este punto se construye el prototipo que permita comprobar que efectivamente el diseño realizado funciona correctamente en el sistema real.
Pudiera ocurrir que aparezcan problemas no previstos que obliguen a reconsiderar varias decisiones anteriores (sensor, actuador, control, etc.). Pudiera ocurrir asimismo, que no sea posible construir un prototipo para probar el diseño, y tenga que ser suficiente la simulación de todo el proceso (por ejemplo un satélite, un módulo lunar, etc.).
Como se ha explicado en el apartado 4 del capítulo 7, salvo en casos particulares, en el diseño de sistemas de control se opta por la utilización de controladores estándar, de tal forma que el diseño de los mismos consista en el ajuste de sus parámetros. La experiencia ha demostrado que salvo en muy contadas excepciones, dan muy buen resultado las denominadas acciones básicas de control, que de acuerdo con su modo de funcionamiento o acción se pueden dividir en los siguientes grupos:
Control Proporcional (P)
Control Integral (I)
Control Proporcional-Integral (PI)
Control Proporcional-Derivativo (PD)
Control Proporcional-Integral-Derivativo (PID)
Siendos los cuatro primeros casos particulares del último, como se detalla en las subsecciones que siguen.
El Control Proporcional (P) es la acción de control más sencilla de todas, ya que únicamente amplifica o atenúa la señal de error para generar la señal de control según la ecuación:

siendo K la ganancia del controlador.
Prácticamente en cualquier sistema físico se puede conseguir que el sistema reduzca su error estacionario y sea más rápido, simplemente con aumentar la ganancia del controlador proporcional, pero a costa de inestabilizarlo, ya que llegado un momento el sistema controlado en lazo cerrado puede convertirse en un sistema inestable.
En el controlador de acción integral (I) la señal de control se genera integrando la señal de error según refleja su ecuación diferencial:
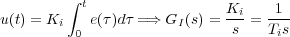
siendo Ti la constante de tiempo de la acción integral. Como es sabido, con la acción integral se mejora el comportamiento del sistema en régimen estacionario. Si a la acción de control del regulador proporcional se le añade una acción que derive la señal de error se obtiene el controlador Proporcional-Derivativo (PD). Es sabido que esta acción le da un carácter anticipativo necesario para mejorar la rapidez de respuesta del sistema. La ecuación que rige su funcionamiento es:
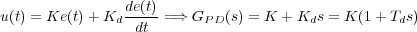
donde K es la ganancia de la acción proporcional, y Td = Kd∕K la constante de tiempo de la acción derivativa.
Si a la acción de control del regulador proporcional se le añade una acción que integre la señal de error se obtiene el controlador Proporcional-Integral (PI). De esta forma se consigue aunar la regulación lo suficientemente rápida que proporciona el control Proporcional, con la precisión en el estacionario del control Integral. La ecuación que rige su funcionamiento es:
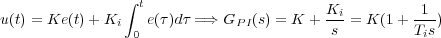
donde K es la ganancia de la acción proporcional, y Ti = K∕Ki la constante de tiempo de la acción integral.
Si se reúnen las tres acciones de control anteriores, esto es, se genera la señal de control a partir de una combinación lineal de la señal de error, su derivada y su integral, según la siguiente ecuación, se obtiene el controlador más general, el Proporcional-Integral-Derivativo (PID), que consigue la rapidez de respuesta de sus partes proporcional y derivativa, y la anulación del error estacionario de su parte integral.
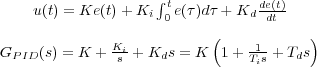
donde K es la ganancia de la acción proporcional, y Td = Kd∕K y Ti = K∕Ki las constantes de tiempo de la acción derivativa e integral, respectivamente.
En la Figura 10.4 se muestra el diagrama de bloques de un sistema en lazo cerrado con control P (Td=0, Ti=∞ ), PI (Td=0), PD (Ti=∞) y PID.
Sin embargo, se observa que los controladores PID estudiados (son ideales) dan lugar a ciertos problemas de estabilidad, sensibilidad, excesivo ancho de banda en algunos casos, etc., y por ello será necesario en muchos casos modificarlos, suavizando sus efectos (ver el Apéndice 2: Modificaciones al control PID).
Si se conoce de forma más o menos exacta un sistema, esto es, su modelo matemático, el diseño de un controlador PID adecuado para que el sistema se comporte en lazo cerrado de la forma deseada es sencillo, y existen varias técnicas para conseguirlo. Ahora bien, si no se conoce de forma precisa, no será posible obtener analíticamente el controlador deseado y será necesario recurrir a aproximaciones experimentales para sintonizarlo.
El proceso de obtener los parámetros adecuados para que se cumplan en lazo cerrado las especificaciones deseadas en el diseño se conoce como sintonía del controlador.
En esta sección se van a estudiar tres métodos de sintonía del PID: Sintonía de Ziegler-Nichols, sintonía en el lugar de las raíces y sintonía manual.
Ziegler y Nichols sugirieron una serie de reglas para sintonizar PIDs basadas en un estudio experimental de múltiples respuestas de sistemas (ante entrada escalón, y estudiando la ganancia de estabilidad crítica en el caso de un sistema con control proporcional).
|
Existen dos métodos llamados reglas de sintonía de Ziegler-Nichols, y en ambos la característica común es que en general se consigue un factor de decaimiento del 25%, esto es, que el valor de la salida ante entrada escalón decae a un cuarto en un periodo de oscilación (Figura 10.5).
En este primer método, se obtiene experimentalmente la respuesta de la planta ante entrada escalón unitario (Figura 10.6).
|
Si la planta, que por supuesto tiene que ser estable, no tiene ni integradores ni parejas de polos complejos conjugados dominantes, entonces la respuesta del mismo tendrá la forma de S (S-shaped). Como inconveniente de este método se puede decir que no es aplicable a sistemas cuya salida no tenga la forma de S.
|
Este tipo de salidas se pueden caracterizar con tres constantes (KLA, L y T) que se pueden obtener gráficamente de la salida del sistema en lazo abierto ante entrada escalón unitario (Figura 10.7). La función de transferencia del sistema se puede aproximar entonces por una de primer orden con retardo de la forma:
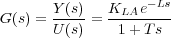
Ziegler y Nichols sugirieron que los valores de los parámetros del PID (K, Td y Ti) más adecuados para este tipo de sistemas son los que se muestran en la Tabla 10.1.
|
Se puede observar que
el PID sintonizado según este primer método tiene un polo en el origen
y un cero doble en s = 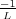 .
.
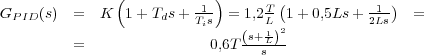
En el segundo método se considera el sistema en lazo cerrado formado por la planta, el controlador PID en serie y realimentación unitaria. Se hace Ti = ∞ y Td = 0, esto es, se activa únicamente el control proporcional, y se va incrementando la ganancia proporcional K desde cero hasta el valor de la misma (Kcr) que haga al sistema críticamente estable, y por lo tanto presente la salida una oscilación mantenida (ante entrada tipo escalón).
Este método no puede aplicarse si no existe un valor de la ganancia proporcional que haga al sistema críticamente estable.
Además de la ganancia de estabilidad crítica se mide experimentalmente el periodo de oscilación de la señal de salida para dicho valor de la ganancia proporcional (Figura 10.8).
Y con estos dos valores, Ziegler y Nichols sugirieron que los parámetros del PID más adecuados para este tipo de sistemas son los que se muestran en la Tabla 10.2.
|
Se puede observar que
el PID sintonizado según este segundo método tiene un polo en el origen
y un cero doble en s = 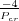 .
.
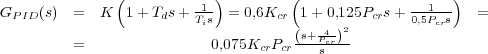
Los valores obtenidos con cualquiera de los dos métodos de sintonía de Ziegler-Nichols no aseguran un comportamiento óptimo, simplemente son en la mayoría de los casos una buena aproximación al control ideal. Por ello será necesario realizar un reajuste de los parámetros del PID con otros métodos para mejorar la dinámica del sistema realimentado.
Cuando las especificaciones deseadas para un sistema de control vienen dadas en el dominio temporal, el procedimiento gráfico de diseño más adecuado es el método del lugar de las raíces.
En definitiva el diseño de un sistema de control consiste en que éste cumpla una serie de requisitos en los regímenes transitorio y permanente. Normalmente las especificaciones están definidas para entradas sencillas como son el escalón o la rampa unitarias.
La experiencia ha demostrado que la respuesta al escalón unitario de un sistema puede considerarse como aceptable, cuando es semejante a la de un sistema de segundo orden cuyo coeficiente de amortiguamiento está comprendido entre δ = 0,3 y δ = 0,8, esto es, con reboses comprendidos entre el 35 % y el 5 %. Reboses superiores al 35 % han de ser amortiguados por ser demasiado oscilatorios, e inferiores al 5 % acelerados por ser demasiado lentos y amortiguados.
Para juzgar el comportamiento del sistema en régimen estacionario se estudian las constantes de error o coeficientes estáticos de error (Kp, Kv y Ka). Dado que cuanto mayores sean estos coeficientes menores serán los errores asociados, el diseño estará encaminado a aumentar dichos coeficientes.
El hecho de haber elegido el escalón unitario como entrada para definir un buen comportamiento del sistema es meramente empírico, ya que se ha comprobado que si la respuesta del sistema ante dicha entrada es adecuada, y el error es suficientemente pequeño, el sistema responderá aceptablemente ante cualquier entrada.
Es importante decir que el regulador PD se utiliza para mejorar el régimen transitorio del sistema, y el PI para la parte estacionaria. El PID, evidentemente, se utiliza para mejorar ambas partes.
Por último es de desear que el sistema sea estable en lazo abierto con cualquier controlador que se diseñe para que en caso de abrirse el lazo de control por alguna razón, el sistema siga siendo estable y no suponga accidentes ni roturas de algún dispositivo del lazo en estos casos.
Por supuesto no es necesario decir que lo primero que habrá que hacer es comprobar si con un mero control proporcional se cumplen las especificaciones deseadas, y si así fuera no sería necesario continuar con controladores más complejos.
Para estudiar el método de ajuste de los parámetros del control tipo PID se va a considerar un sistema cuya función de transferencia es G(s) y con una realimentación H(s). Por lo tanto la función de transferencia en lazo abierto (sin incluir el controlador) será G(s)H(s).
Si las especificaciones deseadas del sistema implican que los polos del mismo sean unos dados (por ejemplo, s1 en la Figura 10.9), habrá que conseguir que el lugar de las raíces pase por ese punto, esto es, que el punto s1 pertenezca al lugar de las raíces.
|
Por tanto, si s1 pertenece al lugar de las raíces tiene que cumplir la condición del argumento:
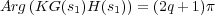
radianes:
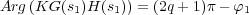
Por lo tanto
será necesario añadir φ1 radianes al argumento de la función de
transferencia en lazo abierto. Para ello se coloca un cero en s = -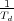 tal que φ =
φ1
(Figura 10.9 ), y
de esta forma se cumple la condición del argumento para s1, y con
ello se consigue que pertenezca al lugar de las raíces. Y como el
controlador proporcional-derivativo es el que añade un cero en la
función de transferencia en lazo abierto, se tiene:
tal que φ =
φ1
(Figura 10.9 ), y
de esta forma se cumple la condición del argumento para s1, y con
ello se consigue que pertenezca al lugar de las raíces. Y como el
controlador proporcional-derivativo es el que añade un cero en la
función de transferencia en lazo abierto, se tiene:
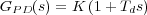
En resumidas cuentas la constante derivativa Td se elige tal que el cero del controlador añada φ1 radianes a la condición del argumento de la función de transferencia en lazo abierto. Y finalmente, mediante la condición del módulo se obtiene la ganancia del controlador que hace que s1 sea polo del sistema en lazo cerrado.
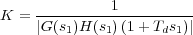
Hay que hacer notar que si se va a incluir la acción integral no será necesario calcular la ganancia proporcional en este momento, dado que posteriormente habrá que reajustarla. De todas formas es conveniente hacerlo para analizar el efecto de la acción derivativa en la dinámica del sistema y compararla con la del sistema controlado con el PID definitivo.
El diseño de la parte derivativa del control PID se ha hecho de tal forma que se escoge la respuesta transitoria (se eligen los polos en lazo cerrado que representan la dinámica deseada), dejando la precisión del sistema (error en régimen permanente) dependiente del diseño del PD realizado. Se podría haber hecho el diseño de forma inversa, esto es, elegir un error en régimen permanente con lo que quedaría fijada la constante proporcional y dejando la otra constante del PD (Td) para que se cumplan otras especificaciones (apoyándonos en el contorno de las raíces, por ejemplo).
Una vez diseñado el controlador PD que ha permitido
elegir un transitorio adecuado para la respuesta del sistema en lazo
cerrado, se puede desear mejorar el régimen estacionario del mismo.
Para ello será necesario introducir un polo en el origen si se quiere
anular errores o convertirlos en finitos si eran infinitos, o una red
de atraso (GAT = K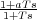 con a < 1)
si lo que se desea es únicamente reducir el error a valores más
aceptables.
con a < 1)
si lo que se desea es únicamente reducir el error a valores más
aceptables.
El controlador PI es precisamente el que permite introducir un polo en el origen:
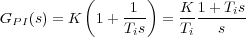
Para conseguir que el
transitorio del sistema no se modifique, o se modifique poco (se supone
que se ha diseñado un PD que fije el transitorio a uno deseado), se
sitúa el cero (-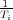 )
muy cerca del eje imaginario (del origen), y con ello el ángulo φ será muy pequeño (Figura 10.10), y por lo
tanto el punto s1 seguirá perteneciendo al lugar de las
raíces, y con ello se habrá conseguido no modificar en exceso el
transitorio del sistema.
)
muy cerca del eje imaginario (del origen), y con ello el ángulo φ será muy pequeño (Figura 10.10), y por lo
tanto el punto s1 seguirá perteneciendo al lugar de las
raíces, y con ello se habrá conseguido no modificar en exceso el
transitorio del sistema.
|
El permanente por el contrario se ha modificado al haber añadido un integrador o polo en el origen en la función de transferencia en lazo abierto (se ha aumentado el tipo del sistema con lo que ello supone en la capacidad del sistema en seguir a mayor número de señales de entrada, como se estudió en el Capítulo 8).
En la función de transferencia en lazo cerrado aparecerá una pareja de polo-cero muy cerca del origen (dominantes) (Figura 11.11). Pero como están muy cercanos entre sí, el residuo correspondiente a dicho polo será pequeño, y por lo tanto su influencia en el transitorio será, asimismo, muy pequeña.
|
Anteriormente se ha llegado a la conclusión de que para no alterar en exceso el transitorio de la salida del sistema, el cero del controlador se ha de colocar muy cerca del origen. Existen dos opciones (Figura 10.12) que permiten cuantificar dicha cercanía:
Si la función de transferencia en lazo abierto tiene un polo en el origen se procede de la misma forma (Figura 10.13 ).
|
Finalmente, faltaría retocar la ganancia de la función de transferencia en lazo abierto para mantener el error en régimen permanente.
La función de transferencia en lazo abierto sería
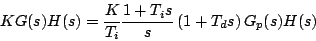
Y por lo tanto, considerando que el sistema fuera de tipo 0 (sin polos en el origen), la señal de error en el régimen permanente se obtendría a partir de los coeficientes estáticos de error que serían en este caso:
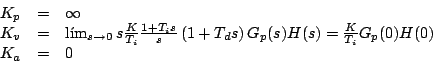
Con lo que se ha conseguido, suponiendo que el sistema en lazo cerrado sea estable, anular la señal de error en el permanente ante entrada escalón y hacerla finita ante entrada rampa.
Por otra parte se
puede observar que al ser el tiempo integral Ti grande
(-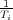 cercano al origen) el coeficiente estático de error de velocidad Kv ha
disminuido, y por lo tanto el error ante entrada rampa ha aumentado.
Esta aparente contradicción no es tal, ya que se ha introducido un
control PI o lo que es lo mismo un polo en el origen, que, como se
explicó en el Capítulo 8, consigue que el sistema siga a una
entrada de mayor orden que la que se podía sin la aplicación del
controlador integral.
cercano al origen) el coeficiente estático de error de velocidad Kv ha
disminuido, y por lo tanto el error ante entrada rampa ha aumentado.
Esta aparente contradicción no es tal, ya que se ha introducido un
control PI o lo que es lo mismo un polo en el origen, que, como se
explicó en el Capítulo 8, consigue que el sistema siga a una
entrada de mayor orden que la que se podía sin la aplicación del
controlador integral.
Si se desea disminuir
la señal de error ante, por ejemplo, una entrada rampa, será a costa de
modificar la respuesta transitoria. En definitiva se tratará de alejar
el cero introducido por el controlador -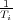 del origen, aumentar con ello la contribución φ de dicho cero a la condición del argumento, y
por lo tanto se modifica el lugar de las raíces. Y, como en casi todos
los problemas de diseño de sistemas de control, habrá que optar por una
solución de compromiso, en la que se sacrifican algunas
especificaciones para conseguir un diseño en general satisfactorio.
del origen, aumentar con ello la contribución φ de dicho cero a la condición del argumento, y
por lo tanto se modifica el lugar de las raíces. Y, como en casi todos
los problemas de diseño de sistemas de control, habrá que optar por una
solución de compromiso, en la que se sacrifican algunas
especificaciones para conseguir un diseño en general satisfactorio.
Existen infinidad de formas de sintonizar los parámetros de un controlador PID además de los dos métodos vistos. Uno de ellos es un método absolutamente empírico que permite fijar las constantes del controlador de una forma totalmente manual, y que puede ser aplicado por operarios sin ningún conocimiento ni en la Teoría de Ingeniería de Sistemas ni en el propio sistema físico que se desea controlar.
Los pasos de diseño son:
Este método es por supuesto un ejemplo de diseño absolutamente empírico, que no vale para muchos sistemas de control, y que no es óptimo bajo ningún sentido. Únicamente puede servir como ilustración de la forma de diseñar sistemas de control sencillos, para los cuales las especificaciones requeridas sean muy abiertas y de mínima exigencia y por todo ello no requieran un control muy preciso.
Debido a que el control derivativo provoca una función impulso ante un cambio brusco en la entrada al controlador (por ejemplo una señal escalón), se hace conveniente modificarlo por un control cuya función de transferencia sea:
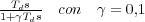
De tal forma que ante un cambio brusco en la entrada se puede suavizar la señal de salida del controlador sin más que elegir un valor adecuado del parámetro γ (Figura 10.14). Aún así, la presencia del control proporcional en la cadena directa sigue trasladando a la salida del controlador los cambios bruscos que se produzcan en la entrada al mismo.
Para evitar este problema, que es un problema en el sentido de que si se somete a un sistema a cambios bruscos en los valores de sus variables se pueda producir daños en sus componentes, se puede modificar el esquema de control del PID de varias formas, como se ve en el Apéndice 2. Modificaciones al control PID.