|
Figura 3.1: |
Elementos pasivos de los circuitos eléctricos |
Se repasan las ecuaciones dinámicas de varios tipos de sistemas físicos que pueden ser utilizados en un lazo de control, como pueden ser los sistemas eléctricos, mecánicos, electromecánicos (motores, generadores) y térmicos.
3.1 Introducción
3.2 Sistemas eléctricos
3.2.1 Redes pasivas
3.2.2 Amplificador operacional
(AO)
3.3 Sistemas mecánicos
3.3.1 Movimiento de traslación
3.3.2 Movimiento de rotación
3.3.3 Conversión
traslación-rotación
3.3.4 Tren de engranajes, poleas y
palancas
3.4 Sistemas electromecánicos
3.4.1 Motor de corriente continua (cd)
controlado por inducido
3.4.2 Motor cd controlado por
campo
3.5 Sistemas térmicos
El objetivo de un sistema de control no es otro que conseguir que la señal de salida de un sistema dinámico (la velocidad angular de un motor eléctrico, la orientación de una antena, el vector velocidad de un aeroplano, etc.) alcance un valor deseado de una determinada forma, a pesar de que sobre dicha señal o sobre otra parte del sistema actuen una serie de fuerzas perturbadoras externas o se produzcan una serie de cambios de parámetros internos en el mismo. Sin embargo, antes de cualquier problema de diseño es necesario disponer de un modelo del sistema a controlar para poder analizarlo y mediante la simulación del modelo obtenido comprobar si es admisible o no.
La modelización de sistemas dinámicos complejos es, en general, muy difícil, lenta y costosa. En este capítulo se van a estudiar los principios más elementales que permitan plantear las ecuaciones de la dinámica para sistemas simples: eléctricos, mecánicos, electromecánicos y térmicos.
Una vez obtenido el modelo matemático de un sistema de control, generalmente ecuaciones diferenciales ordinarias, será necesario resolverlas para analizar la respuesta dinámica del sistema y posteriormente plantear el diseño de control más adecuado. En general la resolución de ecuaciones dinámicas de sistemas reales es muy compleja dado que se trata de ecuaciones de alto orden, variables en el tiempo y no lineales. En control, sin embargo, la finalidad del mismo suele consistir en mantener la señal de salida del sistema en un punto de equilibrio, y de esta forma es posible estudiar el comportamiento del sistema en torno a este punto y ante señales de entrada de pequeño valor. Como consecuencia, en muchos casos, es posible simplificar las ecuaciones a un modelo lineal invariante en el tiempo.
Los circuitos eléctricos se componen de interconexiones de fuentes de voltaje y corriente eléctrica, elementos pasivos como resistencias, condensadores e inducciones, y elementos electrónicos activos, especialmente amplificadores operacionales. Antes de la llegada de los ordenadores estos elementos eran prácticamente los únicos que permitían la construcción de dispositivos de control, y concretamente los amplificadores operacionales han permitido simplificar enormemente el diseño de controladores.
La forma clásica de escribir ecuaciones de circuitos eléctricos se basa en el método de mallas o en el de nodos, los cuales están formulados a partir de las dos leyes de Kirchoff:
Leyes de corriente de Kirchoff: La suma algebraica de todas las corrientes que dejan un punto de unión o nodo en un circuito es cero.
En este apartado se van a estudiar las redes pasivas básicas de uso más frecuente en los circuitos eléctricos que forman parte de los sistemas de regulación automática: resistencias, condensadores y bobinas.
|
En la Figura 3.1 se pueden ver estos elementos, sus ecuaciones, y en la Tabla 3.1 se muestran los símbolos y unidades utilizados en los sistemas eléctricos.
|
En el procesamiento de señal y en circuitos para control de sistemas la finalidad más común de los circuitos electrónicos es la amplificación de señal, y para ello se utiliza de forma generalizada el amplificador operacional (AO). Aunque no es labor de esta asignatura el profundizar en el estudio de estos dispositivos, dada la utilización de los mismos en la Ingeniería de Control se va a proceder a realizar una breve introducción.
Aún cuando el AO esté formado internamente por transistores y resistencias conectados entre sí de manera compleja, sus características externas, que son los que realmente interesan en la Ingeniería de Control, son relativamente simples. De hecho, el AO se puede estudiar únicamente desde un punto de vista externo, considerándolo como una “caja negra”, y siendo representados por modelos lineales muy simplificados.
|
El símbolo del AO se muestra en la Figura 3.2. La ganancia a baja frecuencia Ao de los amplificadores comerciales van desde 105 hasta 107, considerándose a efectos prácticos como infinito, sin con ello perder exactitud en los cálculos. Ésta sería una de las aproximaciones que se realizan al modelizar lo que se denomina el AO ideal, y que se detallan a continuación:
El voltaje entre las terminales + y - es cero, esto es, v+ = v-. Esta propiedad se conoce como tierra virtual o corto virtual.
Las corrientes dentro de las terminales + y - son nulas. Por tanto, la impedancia de entrada es infinita.
La impedancia vista hacia la terminal de salida es cero. Por tanto, la salida es una fuente de voltaje ideal.
La relación entrada-salida es vo = Ao(v+ - v-), donde la ganancia Ao tiende a infinito.
La aplicación de estas aproximaciones hace posible la construcción de múltiples configuraciones donde esté presente el AO. Ahora bien, hay que adelantar que no es posible utilizar un AO tal como se muestra en la Figura 3.2, sino que es necesario añadir realimentación de la señal de salida del mismo (vo) hacia la terminal de entrada v-.
En capítulos posteriores se verá que en la construcción de reguladores de sistemas de control se utilizan de forma habitual circuitos que multipliquen, deriven o integren una señal. Dichos circuitos se pueden construir de una forma muy sencilla mediante AO. En el Apéndice 1 se muestran sencillos circuitos con AO que realizan alguna de dichas operaciones básicas.
El movimiento de los elementos mecánicos de un sistema de control puede ser de traslación, de rotación o una combinación de ambos. En cualquier caso, cualquiera de ellos actúa de acuerdo a las leyes de Newton.
El movimiento de traslación está definido como un movimiento que se realiza en linea recta. Las variables que permiten su descripción son desplazamiento, velocidad y aceleración lineales. La segunda ley de Newton aplicada a un cuerpo rígido en movimiento de traslación se puede expresar de la forma:
![]()
esto es, la suma algebraica de las fuerzas que actúan sobre el cuerpo en una dirección dada es igual al producto de su masa M por su aceleración a en la misma dirección.
Los elementos básicos que intervienen en un sistema mecánico de traslación son: masa, resorte lineal o muelle y fricción o rozamiento viscoso. Dichos elementos, junto con sus ecuaciones, son mostrados en la Figura 3.3 mientras que en la Tabla 3.2 se incluyen los símbolos y unidades empleadas para las diversas magnitudes que intervienen en este tipo de sistemas.
|
|
El movimiento de rotación de un cuerpo se puede definir como su giro alrededor de un eje fijo. La segunda ley de Newton para el movimiento de rotación es:
![]()
que establece que la suma algebraica de los momentos o pares alrededor de un eje fijo es igual al producto del momento de inercia J por la aceleración angular α alrededor del eje.
Los elementos básicos que intervienen en un sistema mecánico de rotación son: inercia, resorte torsional o rigidez y fricción o rozamiento viscoso. Dichos elementos y sus correspondientes ecuaciones son mostrados en la Figura 3.4 mientras que en la Tabla 3.3 se incluyen los símbolos y unidades empleadas para las diversas magnitudes que intervienen.
|
Figura 3.4: Elementos mecánicos de rotación |
En sistemas de control de movimiento es habitualmente necesario convertir movimientos de rotación en movimientos de traslación. Así, por ejemplo, es común desplazar cargas a lo largo de una línea recta mediente el uso de un tornillo sinfín, un sistema de cremallera o una polea movidos todos ellos por un motor (Figuras 3.5).
|
Estos dispositivos se pueden representar por un sistema simple con una inercia equivalente conectada directamente al motor. Por ejemplo, la masa que desplaza el piñón que mueve la cremallera o la que desplazan los motores que mueven las poleas de las Figuras 3.5.b y 3.5.c, respectivamente, se puede representar con una inercia equivalente conectada directamente al motor. De tal forma que si se desprecia la inercia asociada al propio piñón o a la polea, la inercia equivalente que el motor mueve sería:
|
(3.1) |
siendo r el radio del piñón o la polea, W el peso de la masa M que se desplaza y g la aceleración de la gravedad. En el caso del tornillo sinfin de la Figura 3.5.a, si se define L como la distancia lineal que la masa se desplaza por cada vuelta del tornillo la ecuación (3.1) es igualmente válida, quedando la inercia equivalente:
![]()
En los sistemas de control es común la necesidad de introducir mecanismos que transmitan energía desde una parte del sistema a otro en una forma tal que se alteran la fuerza, el par, la velocidad y el desplazamiento. Un ejemplo típico son los trenes de engranajes que se acoplan entre el eje de un servomotor y la carga que mueve. Su efecto es conseguir la reducción de la alta velocidad de giro del eje del motor junto con un aumento del par útil disponible en la carga.
|
Figura 3.6: Tren de engranajes |
En la Figura 3.6 se pueden observar dos engranajes acoplados. En un primer estudio se considera que la inercia y rozamiento de los mismos es despreciable, el rendimiento de la transmisión es perfecto y que el motor y el tren de engranajes han sido diseñados para que proporcionen el par, la aceleración y velocidad necesarios en la carga. En consecuencia, el dispositivo actúa según los siguientes principios:
El número de dientes de cada engranaje es proporcional al radio del mismo:
![]()
siendo N1 y N2 el número de dientes, respectivamente, de los dos engranajes, y r1 y r2 los radios de los mismos.
La distancia lineal recorrida sobre la periferia de cada engranaje es la misma:
![]()
siendo θ1 y θ2, respectivamente, los ángulos girados por cada engranaje.
El trabajo realizado por un engranaje es igual al realizado por el otro (se supone que no hay pérdidas):
![]()
siendo T1 y T2, respectivamente, los pares desarrollados por los dos engranajes.
Entonces, si las velocidades angulares de los engranajes son, respectivamente, ω1 y ω2 de las ecuaciones anteriores resultan las siguientes relaciones:
![]()
En la práctica los trenes de engranajes tienen inercia y rozamientos entre los dientes de los mismos que a menudo no se pueden despreciar. Por tanto, las relaciones anteriores no son tan sencillas.
Los sistemas electromecánicos de regulación son aquellos que utilizan elementos que convierten la energía eléctrica en mecánica o viceversa. Entre los más utilizados actualmente están los motores y los generadores de corriente continua (cd). En este apartado se van estudiar los motores de cd controlados por el inducido, armadura o rotor y los motores de cd controlados por el campo de excitación o inductor. El uso de este tipo de motores se ha ido imponiendo con respecto al uso de los motores de corriente alterna (más eficaces en tiempos pasados) por varios motivos, entre ellos:
Los motores de corriente alterna son más difíciles de controlar, especialmente para control de posición.
Los avances logrados en electrónica de potencia han hecho que los motores cd sin escobillas sean muy populares en sistemas de control de alto desempeño.
En este apartado se van a estudiar de una forma breve los motores cd de imán permanente o controlados por el inducido, armadura o rotor. La Figura 3.7 muestra el rotor y el estátor de un motor cd de este tipo junto con un esquema simplificado que lo representa.
|
Figura 3.7: Rotor y estátor de un motor cd de imán permanente y esquema equivalente |
Las diferentes variables y parámetros del motor se definen como sigue:
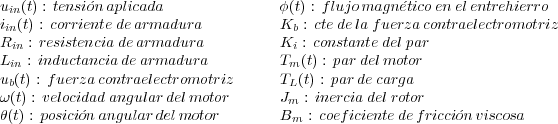
Para obtener unas ecuaciones lineales que reflejen el comportamiento del motor cd controlado por el inducido se pueden realizar una serie de supuestos, que sin ser exactos pueden considerarse como aceptables en la mayoría de los casos:
La armadura o inducido está modelado como una resistencia (Rin) en serie con una inductancia (Lin), y una fuente de voltaje (ub(t)) que representa la fuerza contraelectromotriz que se induce en la armadura al girar el rotor.
La fuerza contraelectromotriz anterior es proporcional, con una constante de proporcionalidad Kb, a la velocidad de rotación del eje del motor (ω(t)).
El circuito de excitación del campo se puede simplificar con una resistencia (Rex) y una inductancia (Lex).
La intensidad de excitación del campo (iex) se puede considerar constante.
El flujo del entrehierro (Φ) es proporcional a la intensidad de excitación (iex).
El par desarrollado por el motor (Tm(t)) es proporcional al flujo en el entrehierro (Φ) y a la intensidad de inducido (iin(t)).
Los elementos mecánicos se pueden modelar mediante una inercia de momento Jm y un rozamiento viscoso de constante Bm.
Aplicando las aproximaciones anteriores se puede obtener la siguiente relación de ecuaciones que definen el comportamiento del modelo del motor cd controlado por inducido o armadura:
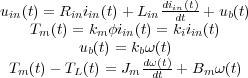
Aplicando la transformada de Laplace a las ecuaciones anteriores se tiene:
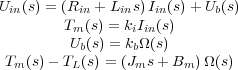
Por último, se pueden representar estas expresiones de forma gráfica mediante diagramas de bloques, como se observa en la Figura 3.8. Este tipo de diagramas presentan la ventaja de dar una visión global y clara del funcionamiento del motor y de las relaciones entre las diferentes variables.
|
Figura 3.8: Diagrama de bloques de un motor cd controlado por armadura |
A diferencia de los motores cd controlados por el inducido o armadura, en los controlados por el campo de excitación la intensidad del inducido es constante, y por ello el par motor es proporcional a la intensidad de excitación de campo. La figura 3.9 muestra el esquema simplificado de un motor de cd de este tipo.
|
Figura 3.9: Esquema de un motor cd controlado por campo o inductor |
A partir de dicho esquema, y teniendo en cuenta que las aproximaciones utilizadas en el motor cd controlado por armadura son igualmente válidas, las ecuaciones que modelan el comportamiento del motor son:
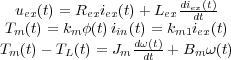
Aplicando la transformada de Laplace se tiene:
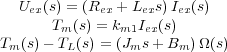
De forma gráfica, mediante diagramas de bloques, el esquema de funcionamiento del motor cd controlado por el inductor o campo de excitación se observa en la Figura 3.10.
|
Figura 3.10: Diagrama de bloques de un motor cd controlado por campo o inductor |
Se puede observar una diferencia clara entre los dos motores estudiados, y es que mientras en el primero aparece una realimentación interna (fuerza contraelectromotriz), el diagrama de bloques del segundo es un esquema en lazo abierto. Esta realimentación interna viene a ejercer de “fricción eléctrica”, y su efecto es tender a estabilizar el motor cd controlado por inducido. Dado que dicho lazo de realimentación no aparece en el controlado por campo, éste tiene un funcionamiento menos estable, y por tanto es más difícil de controlar que el primero.
Considerando la aproximación de que la temperatura de un cuerpo es uniforme en todo él, se pueden estudiar infinidad de sistemas térmicos cuyas ecuaciones diferenciales sean lineales. Un ejemplo clásico y que sirve de base a cualquier sistema de este tipo es el intercambiador de calor de la Figura 3.11.
|
Figura 3.11: Intercambiador de calor: caldera calefactora de un edificio. |
Se trata de un tanque con agua a una temperatura Tt aislada térmicamente del exterior, con una entrada de agua fría y una salida de agua caliente a temperaturas Tf y Tc, respectivamente. En la caldera el agua se calienta mediante un elemento calefactor, y se supone que el agua de la caldera está perfectamente mezclada y por ello la temperatura de la misma es uniforme.
La ley de la conservación de la energía establece que la energía introducida en el sistema (Qf + Qr) ha de ser igual a la almacenada (Qa) más las pérdidas (Qc + Qp), que matemáticamente se expresa:
|
(3.2) |
donde Qr es el flujo de calor aportado por el calentador, Qa el absorbido por el agua del tanque, Qc y Qf los correspondientes al agua caliente y fría que sale y entra a la caldera, respectivamente, y Qp el flujo de calor que se pierde a través del aislamiento.
Teniendo en cuenta las conocidas relaciones de Termotécnia:
|
(3.3) |
donde C = MH es la capacidad térmica del agua del tanque, M la masa de agua, H el calor específico del agua, V el flujo de agua caliente que sale del tanque (que en este ejemplo coincide con el flujo de agua fría que entra a dicho tanque) y R la resistencia térmica del aislamiento (constante cuando la transmisión de calor se realiza por conducción o convección).
Sustituyendo las ecuaciones 3.3 en 3.2 y teniendo en cuenta que en este ejemplo concreto V = cte y Te = Tf (es decir, la temperatura del agua que entra al tanque es igual a la temperatura en el exterior), se tiene:
|
(3.4) |
siendo Tu = Tt -Te la temperatura del agua de la caldera referida a la temperatura exterior. Dicha ecuación diferencial refleja la dinámica del sistema térmico descrito.