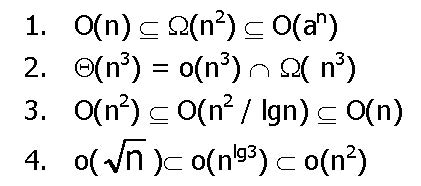- Partiketa mota inplementatzeko ikusitako aukera desberdinen artean eraginkorrena:
- Multzoak zuhaitz bitar ia-beteak taulen bidez inplementatzea da.
- Multzoko etiketak multzoko osagai txikienak izatea da.
- Multzoetako bategitea hauek inplementatzen dituzten zuhaitzen sakonerak kontuan izanik egitea da.
- Multzo bakoitza etiketa duen taula desberdin batean jasotzea da.
- Grafo zuzendu bat matrize bidezko adierazpenetik auzokideen listen bidezko adierazpenera bihurtua izateko
- Ez da beharrezkoa matrizeko posizio guztiak aztertzea; nahikoa da, arkua jasotzen duten posizioak aztertzea.
- Matrize osoa korritu behar da identifikatzeko zeintzuk diren grafoko arkuak. Ondorioz, egingo dugun lanaren denbora-ordena Θ(a2) izango da, non a arkuen kopurua den.
- Derrigorrezkoa da lehendabizi intzidentzia matrize bidezko adierazpidera bihurtzea eta, ondoren, honetatik auzokideen bidezko adierazpenera bihurtzea.
- Beste aukeretatik bat ere ez.
- Grafo bateko bi erpinen artean biderik dagoen erabakitzeko
- sakonerako nahiz zabalerako korritzea erabil dezakegu.
- ezin dugu ez sakonerako ez zabalerako korritzea erabili.
- Soilik zabalerako korritzea erabil dezakegu.
- Soilik sakonerako korritzea erabil dezakegu.
- Programazio dinamikoa memoriadun funtzioak erabiliz inplementzea aproposa da (hots, errekurtsio bidez)
- Memoriako espazio estra aurreztea lortzen baita.
- Soluzioa eraikitzeko metatze egiturako gelaxka asko betetzea beharrezkoa ez denean.
- Metatze egiturako gelaxka guztiak bete behar direnean, oro har, iteratiboki baino azkarrago beteko baititugu.
- Beste aukeretatik bat ere ez.
- Dijkstraren algoritmoak behin A abiapuntutik eta V erpin arteko distantzia berezi motzena soluzioari gehitzen dionean (hots, bide berezi motzena bide motzena bihurtzen duenean):
- Beranduago Atik Vra doan beste bide bat aurkitzen duenean oraingoan soluzioari gehitutako distantzia hori berrikusiko du.
- Vren edozein W erpin auzokiderentzat, A eta W arteko bide motzenak V ez duela zeharkatzen badakigu.
- Vren edozein W erpin auzokiderentzat, A eta W arteko bide motzenak V zeharkatzen duela badakigu.
- Atik Vren auzokideetaraino (W barne) doazen distantzia berezi motzenak hobetzen saiatzen da Dijkstra.
- Teknika jaleari buruzko esaldi hauetatik zuzena aukeratu:
- Une batean baztertutako hautagai bat (hots, prozedurak hautesleak aukeratu du, baina ez da onartu soluzioari gehitzea), ondorengo bira batean berriz ere kontsidera liteke.
- Edozein optimizazio problema teknika jalea erabiliz ebatz liteke.
- Oro har, erraza da prozedura hauteslea ona dela frogatzea.
- Prozedura hautesle bat ona ez dela azaltzeko, soluzio ez optimoak ekoitz ditzakeela erakusten duen kontrako adibidea bilatzen da.
- Backtrack eskema eta honek esploratzen duen zuhaitzei buruzko esaldi hauetatik okerra aukeratu:
- Esplorazio zuhaitza zer-nolakoa den marraztea komeni da backtrack kodea idatzi ahal izateko.
- Problema batek esplorazio-zuhaitz bakarra eduki dezake.
- Heuristiko funtzioek hostoak ez ezik zuhaitzeko adar osoak kima ditzakete.
- Zuhaitzeko erpinen tratamenduak denbora-konstantean egiten badira, orduan zenbat eta zuhaitz txikiagoak eraiki hainbat eta soluzio azkarragoak lortzen dira.
- Erpin guztien arteko distantzia minimoak kalkulatzeko
- Kruskal erabil dezakegu, honen kostua O(a log p) izanik.
- Dijkstra erabil dezakegu, honen kostua Θ(p2) izanik.
- Erpin bakoitza abiapuntutzat harturik, Dijkstra p aldiz aplikatuz lor liteke Θ(p3) ordenan.
- Grafoak derrigorrez konexua eta ez-zuzendua izan behar du.
- Ondorengobaieztapenetatik zein da zuzena? 1, 2, 3 edo 4?