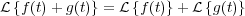
La siguiente tabla provee la mayoría de las transformaciones de Laplace para funciones de una sola variable. Debido a que la transformada de Laplace es un operador lineal, se verifican las siguientes propiedades:
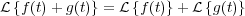
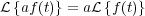
donde a es una constante y, f(t) y g(t) son dos funciones del tiempo.
Además, la transformada de Laplace es únicamente válida cuando t ≥ 0 , lo que explica por qué en la tabla mostrada a continuación todo es múltiplo de la función escalón unitario, denotada por h(t) y definida como:

Aquí está una lista de las transformadas más comunes:
|
En dicha tabla α, τ y ω son números reales, n es un número entero, t denota una variable real, generalmente el tiempo, y s denota una variable compleja.