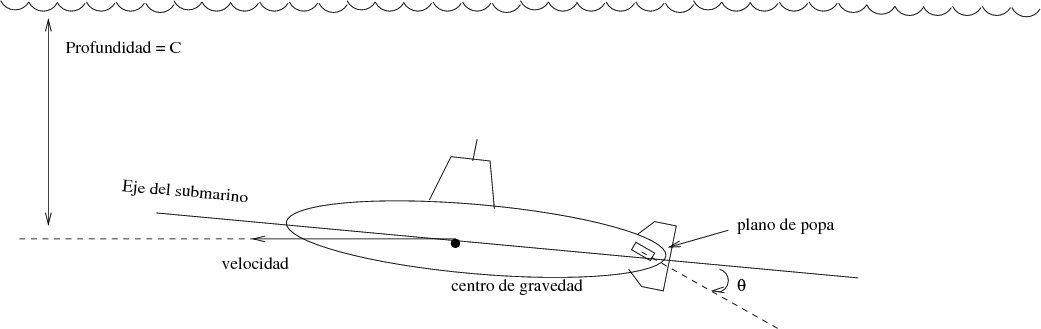
Consideremos el sistema de control automático de profundidad de un submarino, el cual es ilustrado en la siguiente figura:

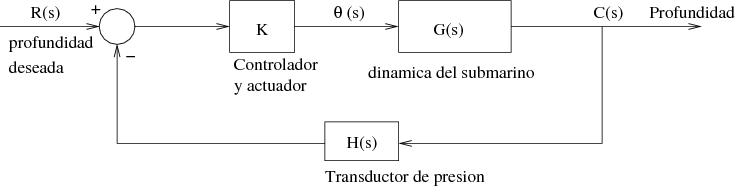
En la práctica, la profundidad actual del submarino es medida mediante un transductor de presión y posteriormente es comparada con la profundidad deseada. La diferencia es amplificada por el controlador que apropiadamente ajustará el ángulo del actuador sobre el plano de popa. El diagrama de bloque del sistema es ilustrado en la siguiente figura:

La dinámica del submarino se puede modelar mediante la función de transferencia G(s) = 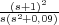, el transductor de presión por H(s) = 1, y para el controlador y actuador se considera una ganancia constante K. Determínese:

1. El lugar de las raíces del sistema con respecto al parámetro K, con K ≥ 0.
2. Describir cualitativamente la dinámica del sistema en función del valor que tome la ganancia K.

Solución:

En este caso la función de transferencia en lazo abierto es:

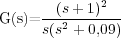
Por tanto, teniendo tres polos, se tienen tres ramas en el lugar de las raíces, que comienzan en los puntos (polos en lazo abierto) s₁ = 0, s_2,3 = ±j0,3 y terminan en los puntos s_4,5 = -1 (cero doble en lazo abierto). Existe una asíntota por ser 1 el exceso polo-cero del sistema. En la siguiente figura se observan los puntos de salida y llegada y el lugar de las raíces en el eje real (pertenece al LR la parte del eje real con un número impar de polos y ceros de la función de transferencia en lazo abierto a su derecha):

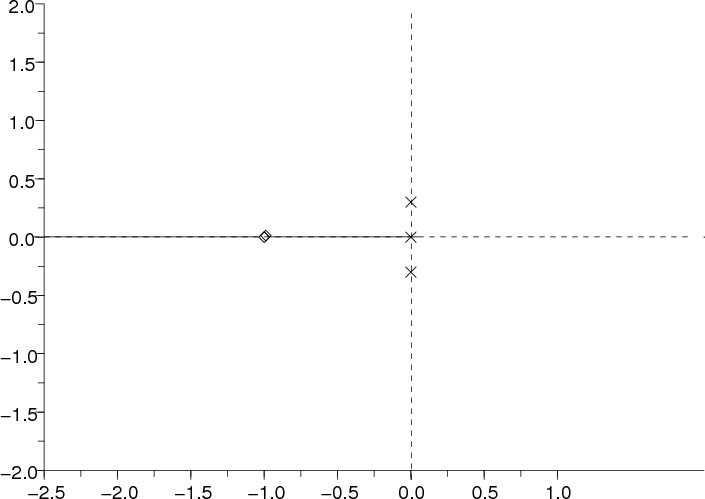
Como se puede observar de la figura, tanto los ángulos de llegada a los ceros, el de salida del polo en el origen y la asíntota no es necesario calcular, ya que se pueden obtener de ésta. Por tanto, se calculan los ángulos de salida de los polos s_2,3 = ±0,3j. Aplicando la condición del argumento

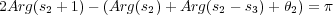
y el ángulo de salida es θ₂ ~ 0,6 rad. Como es lógico, aplicando la propiedad de simetría, θ₃ ~-0,6 rad. A continuación, se calculan los puntos de dispersión y confluencia. Estos deben cumplir inicialmente la siguiente ecuación

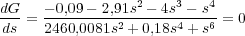
Por tanto, las soluciones posibles son: -1, -3.04, 0.0197±0,171j. La dos primeras pertenecen al lugar de las raíces y son puntos de confluencia (el punto -1 es especial, ya que representa el caso límite k→∞). En cambio, los polos complejos conjugados no pueden pertenecer al LR ya que se necesitarían al menos cuatro polos en la función de transferencia en lazo abierto.

Para acabar se deben obtener los puntos de cruce con el eje imaginario, utilizando el criterio de Routh-Hurwitz. En este caso, la ecuación característica en lazo cerrado es s³ + Ks + (2K + 0,09)s + K=0 y de ésta, como todos los coeficientes deben tener el mismo signo, se tiene que se debe cumplir  que K > 0. Completando la tabla de Routh-Hurwitz:

s3	1	2K+0.09
s2	K	K
s1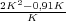
s0	K

Analizando la primera columna se encuentran 2 puntos a estudiar. El primero K=0, donde sólo queda la primera columna y la ecuación auxiliar es s³ + 0,09s = 0, esto es, se cruza el eje imaginario en los puntos 0,±0,03j (son los puntos de partida de las ramas y ya era conocido). El segundo punto a estudiar es K = 0,455, en este caso se hace nula la tercera fila (s¹) y la ecuación auxiliar es s² + 1 = 0, esto es, los puntos de cruce son ±j.

En cuanto a la estabilidad, como ya se ha dicho se debe cumplir K > 0 y analizando el tercer elemento de la primera columna de la tabla K > 0,455. Por tanto, en el rango de valores 0 < K < 0,455 el sistema es inestable, en el punto K = 0,455 críticamente estable y para K > 0,455 el sistema será estable. Con todo esta información se puede dibuljar el siguiente lugar de las raíces.

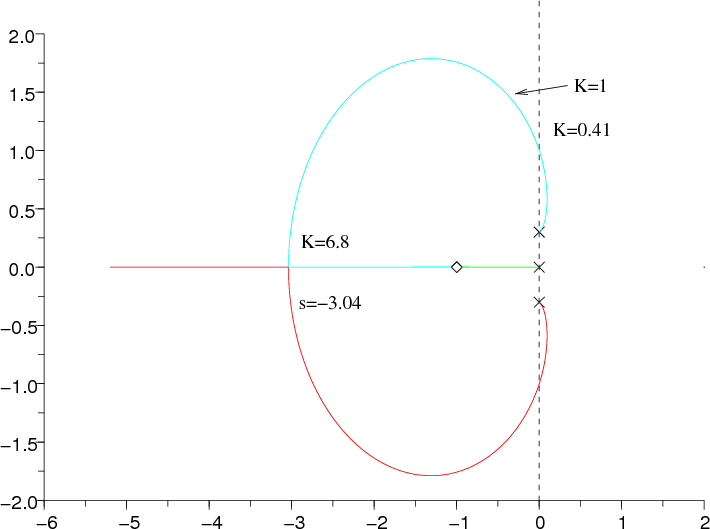
Analizando la dinámica del sistema, el sistema además de ser inestable en el rango 0 < K < 0,455, tiene naturaleza oscilatoria. Como se ha dicho, cuando K = 0,455 el sistema es críticamente estable. Para K > 0,455, siendo el sistema estable, para valores cercanos a ese límite el sistema es muy oscilatorio, creciendo el amortiguamiento de la dinámica según aumenta el valor de K. Al principio, los polos complejos conjugados serán dominantes y el polo que estaba en el origen se acercara a uno de los dos ceros en el punto -1, compensándose. Sin embargo quedará un cero que no será despreciable en ese punto -1, y al alejarse los polos dominantes del eje imaginario irá ganado en importancia (más o menos se debe tener en cuenta para K > 1).

Por otro lado, aumentando K, los polos dominantes se van amortiguando hasta que para K = 6,8 el sistema es críticamente amortiguado, pero con un cero adicional que será importante, aportando un sobreelongamiento a tener en cuenta.

Finalmente, para valores grandes de K se tendrán dos polos, uno que tiende hacia el segundo cero en -1 y otro hacia infinito. Por esa razón ambos van perdiendo importancia, lo cual conduciría a una situación difícil de predecir, donde todos los polos están compensados de alguna forma. Lo más conveniente es realizar cálculos para estar seguro de la dinámica que se presenta, pero se puede esperar que el polo alejado (dinámica rápida) sea dominante en los primeros instantes, siendo el polo que se acerca a -1 (dinámica lenta) el dominante según avanza el tiempo.