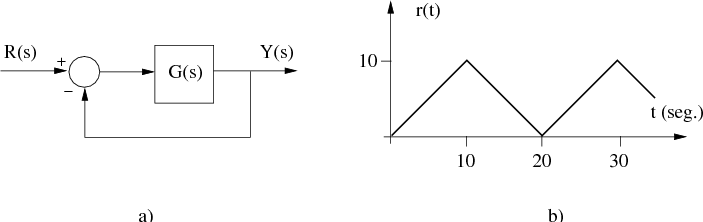
Se programa un robot, cuyo diagrama de control es el de la Figura a), para que, con una herramienta o soplete de soldar, siga la trayectoria dentada que se muestra en la Figura b).

La Función de Transferencia G(s) del sistema de control es:

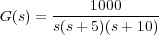
G(s) =-----1000----- s(s+ 5)(s+ 10)

Calcúlese:

El error en régimen estacionario.
Si se añade una ganancia ajustable en la cadena directa, ¿Cuál es el valor de dicha ganancia para la cual el error en régimen estacionario es mínimo?
Dibujar la trayectoria aproximada que seguirá el soplete para este último caso.

Solución:

(i) La señal r(t) aplicada como entrada al sistema de control está formada por tramos tipo rampa de pendientes 1 y -1 distribuidos alternativamente en el tiempo (ver Figura b) ). Por tanto, hay que estudiar el comportamiento en régimen permanente del sistema ante entradas tipo rampa. Este estudio sólo tiene sentido si el sistema es estable, en consecuencia estudiemos la estabilidad del sistema como primer paso para la resolución del problema. Para ello, calculamos la función de transferencia del lazo cerrado a partir del diagrama de bloques de la Figura a):

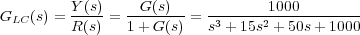
GLC (s) = Y-(s) = --G(s)--= --------1000-------- R(s) 1+ G (s) s3 + 15s2 + 50s+ 1000

A continuación aplicamos el criterio de Routh-Hurwitz al denominador de dicha función de transferencia, es decir, a D(s) = s³ + 15s² + 50s + 1000. Para ello, construimos la tabla de Routh,

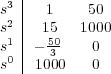
s3| 1 50 s2| 15 1000 s1| - 50- 0 s0| 10300 0

Observando los coeficientes de la primera columna a la derecha de la línea continua de la tabla, se deduce que el sistema posee dos polos inestables al haber dos cambios de signo (de positivo a negativo y de negativo a positivo) en la lista formada por dichos coeficientes. Entonces, no tiene sentido el estudio del régimen permanente del sistema por ser éste inestable.

(ii) Si añadimos una ganancia a la cadena directa, el diagrama de bloques del sistema pasa a ser:

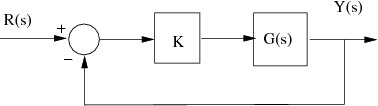
La función de transferencia en lazo cerrado pasa a ser:

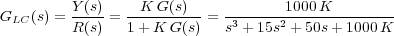
Y(s) -K--G(s)-- --------1000-K--------- GLC (s) = R(s) = 1+ K G (s) = s3 + 15s2 + 50s+ 1000K

Mediante el criterio de Routh-Hurwitz estudiamos el rango de valores de K para los que el sistema es estable. Para ello, construimos la nueva tabla de Routh,

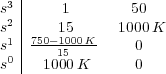
3 | s2 | 1 50 s1 |750--110500K- 1000K s0 | 15 0 s 1000 K 0

La condición necesaria y suficiente para que el sistema sea estable es que los coeficientes de la primera columna a la derecha de la línea continua de la tabla sean positivos, es decir:

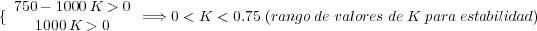
750- 1000K > 0 { 1000K > 0 =⇒ 0 < K < 0.75 (rango de valores de K para estabilidad)

Para este rango de valores de K tiene sentido el estudio del régimen permanente. Ante entradas rampa de pendiente unitaria en valor absoluto (ya que la entrada al sistema está formada por tramos de pendientes 1 y -1) se obtiene el valor absoluto de la señal de error en el estado estacionario a partir de la expresión;

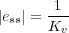
-1- |ess| = Kv

siendo K_v = lim_s→0sK G(s) = 20K. Por tanto,

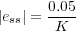
|ess| = 0.05 K

Además, ya que la realimentación es unitaria, la señal de error y el error del sistema coinciden, por tanto;

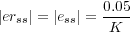
|er | = |e | = 0.05 ss ss K

De esta expresión se deduce que cuanto mayor sea el valor de la ganancia ajustable K menor será el de la magnitud del error en régimen estacionario. Por tanto, el valor de K que hace mínimo el error en el permanente es 0.75. En concreto, para este valor de K el sistema es críticamente estable ya que presenta dos polos sobre el eje imaginario y otro polo dentro del semiplano izquierdo del plano complejo. Para dicho valor de K la magnitud del error es |e_ss| = 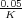0.05 K = 0.066.

(iii) La trayectoria que sigue el soplete si K = 0.75 es:

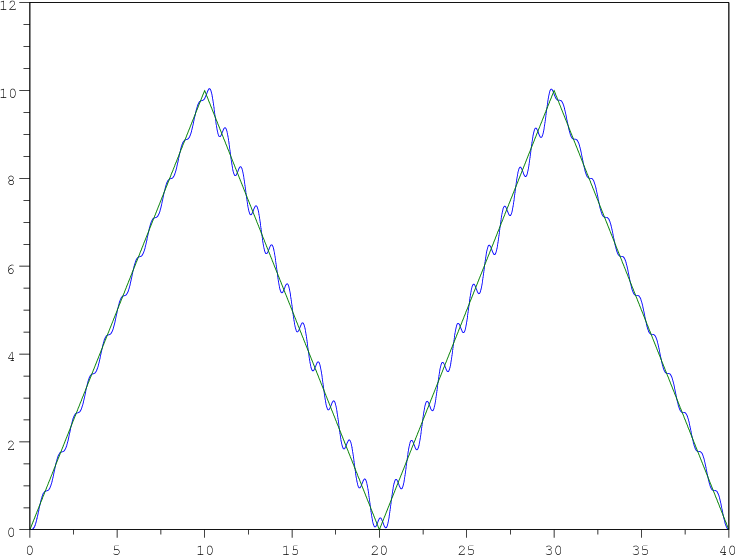
Ya que el sistema es críticamente estable la respuesta del sistema (línea azul) sigue a la de referencia r(t) con oscilaciones en torno a un valor separado ligeramente de dicha señal de referencia (línea verde). En concreto, dicha separación es de magnitud 0.066 una vez alcanzado el régimen permanente (este mismo problema se ha tratado en el ejercicio 2.4).

Si consideramos un valor de K menor, por ejemplo K = 0.5 la respuesta que se obtiene es:

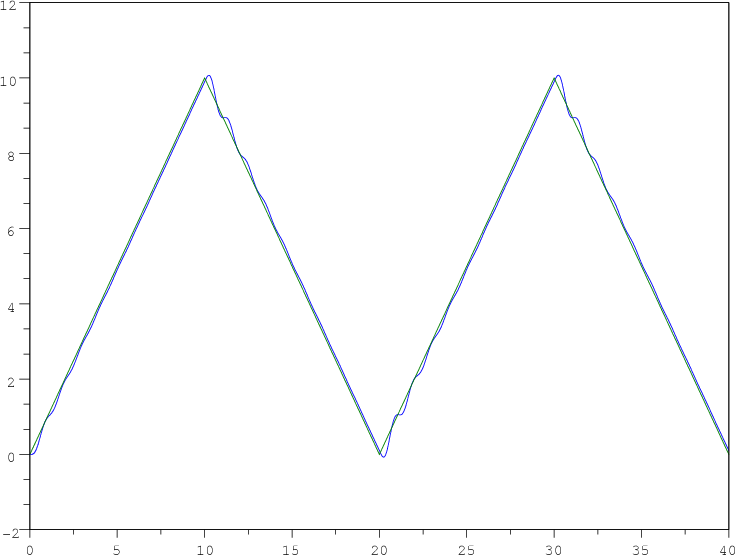
En este caso se observa que una vez alcanzado el regimen permanente la salida del sistema (trayectoria del soplete) sigue a las rampas de la referencia con un pequeño error de magnitud |e_ss| = 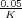0.05 K = 0.1. Se podría apreciar este pequeño error haciendo un zoom en la figura anterior. Y aunque no corresponda al caso de mínimo error, el comportamiento del soplete es mejor que el anterior.