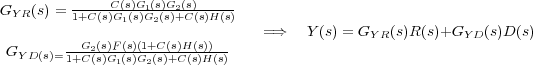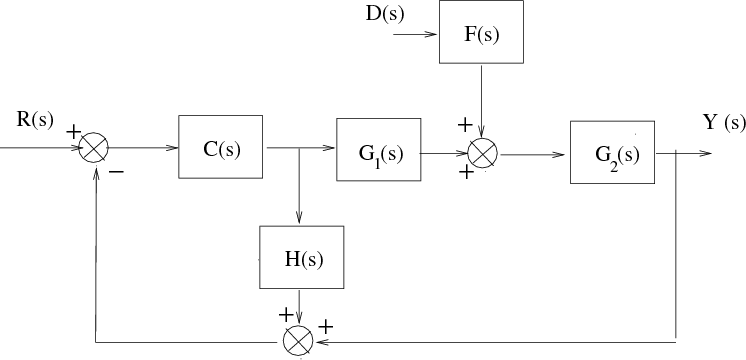
Obtener, mediante reducción de diagrama de bloques, la función de transferencia del sistema de la figura siguiente:

Solución:

Antes de nada hay que definir exactamente lo que se va a obtener. Este sistema tiene dos entradas y una salida, luego tendrá dos funciones de transferencia: una que relaciona la salida con una de las entradas Y(s)/R(s), y otra que la relaciona con la otra entrada Y(s)/D(s).

En primer lugar, para facilitar el trabajo, es conveniente definir las diferentes variables presentes en el diagrama de bloques

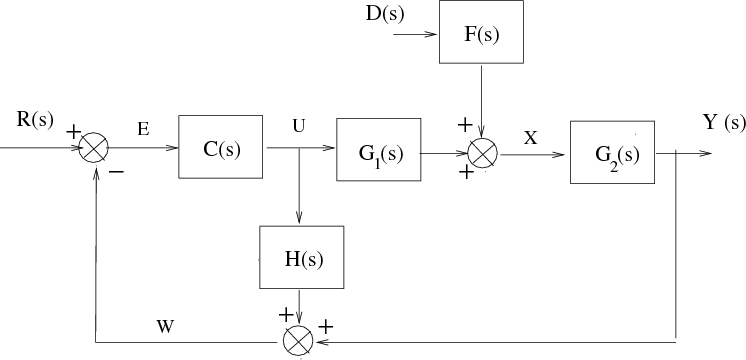
Ahora vamos a desplazar el punto de distribución U hacia la izquierda, saltando el bloque C(s) :

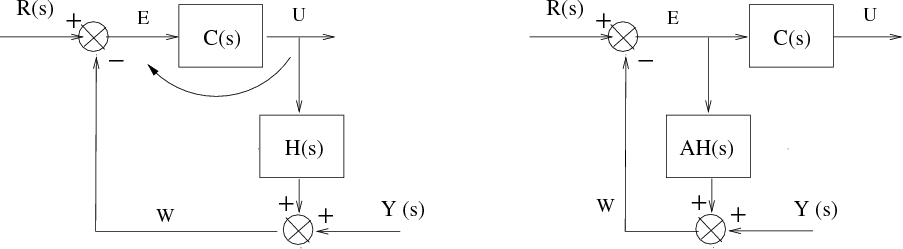
Habrá que calcular entonces el valor de A:

W (s) = Y (s)+ H(s)U(s) = Y (s)+ H(s)C(s)E(s) =⇒ A = C(s) W (s) = Y (s)+ AH (s)E (s)

Eliminamos ahora el lazo que ha surgido:

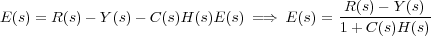
E(s) = R (s)- Y (s) - C (s)H (s)E (s) = ⇒ E(s) =-R(s)--Y(s) 1 +C (s)H (s)

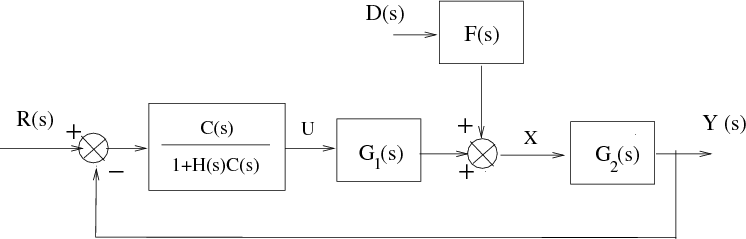
quedando el diagrama de bloques de la figura siguiente:

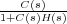A continuación desplazamos también el sumatorio interno hacia la izquierda saltando los bloques G₁(s) y el bloque que ha surgido al eliminar la realimentación interna G₃(s) = 1+CC((ss))H-(s)

. La idea es sacarlo del lazo de realimentación que queda, según la figura:

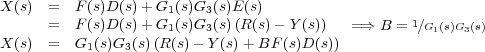
X (s) = F (s)D (s)+ G1 (s)G3(s)E(s) = F (s)D (s)+ G1 (s)G3(s)(R(s)- Y (s)) =⇒ B = 1∕G1(s)G3(s) X (s) = G1 (s)G3(s)(R(s)- Y(s)+ BF (s)D (s))

Por tanto, se tiene el diagrama de bloques

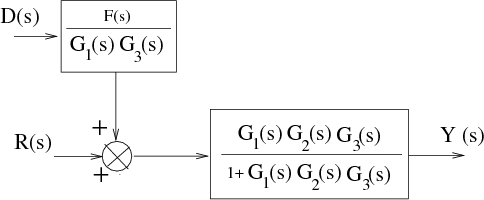
que permite obtener fácilmente la expresión final de la transformada de Laplace Y (s) de la señal de salida que al existir dos entradas, depende de ambas:

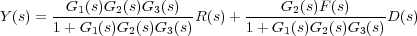
Y (s) =--G1(s)G2-(s)G3-(s)--R(s)+ -----G2(s)F-(s)-----D(s) 1+ G1 (s)G2(s)G3(s) 1 +G1 (s)G2 (s)G3(s)

Y como se ha dicho al inicio, se trata de un sistema MIMO (Multiple Input Multiple Output), y por lo tanto con dos funciones de transferencia que relacionan respectivamente la salida con cada una de las entradas:

C(s)G1(s)G2(s) GYR (s) = 1+C(s)G1(s)G2(s)+C(s)H(s)- =⇒ Y (s) = GYR (s)R(s)+GY D(s)D(s) GYD (s)= 1+GC2((ss))GF1((s)s)(1G+2C(s)(s+)HC((ss))H)(s)