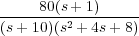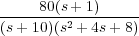Si la función de transferencia de un sistema es G(s) = , obtener un modelo reducido a partir de ésta y explicar de forma cualitativa la salida si se aplica una entrada escalón.

Solución

Analizando la función de transferencia se obtiene la siguiente información:

• Los polos del sistema son s = -10, -2 ± 2j

• El cero del sistema es s = -1

Por su lejanía relativa del eje imaginario del polo situado en -10, éste se puede considerar despreciable y la función de transferencia simplificada puede ser

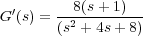
Se debe recordar que la ganancia debe ser ajustada. Por otro lado, para compensar el hecho de eliminar un polo, se puede alejar el cero del eje imaginario para minimizar su influencia.

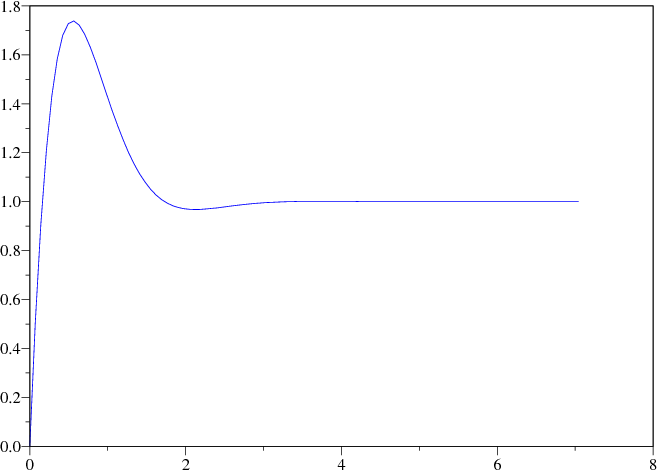
A la hora de aplicar una señal escalón, se debe recordar que se tienen dos polos complejos conjugados dominantes (con δ = 0.707) que confieren a la salida una característica oscilatoria moderada, pero el efecto del cero cercano al eje imaginario añade un gran rebose a la salida. Por otro lado, utilizando las expresiones válidas para un sistema de segundo orden sin cero (como aproximación), el tiempo de pico sería T₁ ~ π∕2 seg. y un tiempo de establecimiento T_p ~ 2 seg.