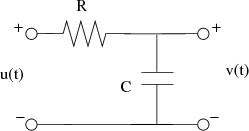
Obtener la función de transferencia del filtro RC de la siguiente figura, así como la de dos de estos filtros puestos en cascada.

Considerando que i(t) es la intensidad que recorre la única malla del circuito, tal y como se observa en la siguiente figura:
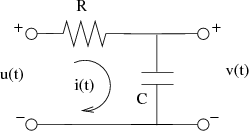
la caída de tensión en la misma u(t) y la que se produce en los bornes del condensador se pueden expresar de la forma:
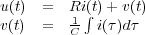
despejando la intensidad
de la segunda ecuación se tiene que la misma es i(t) = C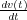 , que sustituyendo en la primera permite
obtener la ecuación diferencial del sistema en función únicamente de
las variables de entrada u(t) y de salida v(t):
, que sustituyendo en la primera permite
obtener la ecuación diferencial del sistema en función únicamente de
las variables de entrada u(t) y de salida v(t):
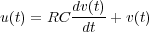
Finalmente, aplicando la transformada de Laplace a la anterior ecuación (considerando las condiciones iniciales nulas) y despejando se tiene la función de transferencia del circuito:
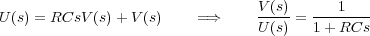
También se solicita obtener la función de transferencia de dos circuitos como el anterior conectados en serie. En un principio se podría tener la tentación de responder que la función de transferencia de dos circuitos conectados en serie sería el producto de sus funciones de transferencia. Sin embargo esta respuesta sería errónea. Se va a resolver el circuito completo como en el caso del circuito simple, obteniéndose la función de transferencia correcta y después se explicará la razón de la no coincidencia entre ésta y la respuesta dada en primer lugar.
De nuevo fijamos las mallas del circuito, que ahora son dos:
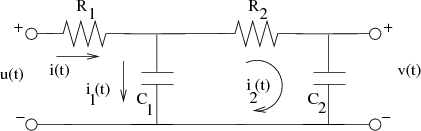
definimos las intensidades que circulan por ellas y directamente se obtienen las ecuaciones que reflejan las caídas de tensión en ambas:
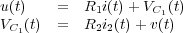 |
(1) |
siendo V C1(t) la caída de tensión en los bornes del primer condensador.
Por otra parte, teniendo en cuenta que la caída de tensión en el segundo condensador se relaciona con la intensidad i2(t) que lo recorre y con la tensión de salida v(t):
 |
(2) |
e igualmente, de la caída de tensión en el primero se obtiene:
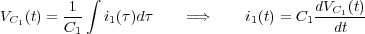
Sustituyendo ahora la segunda de las expresiones (1) y la (2) en la anterior:
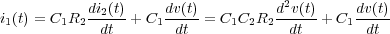
Eliminando la variable V C1(t) en las ecuaciones (1), y sustituyendo las expresiones de las intensidades i1(t) anterior e i2(t) (2 ) se obtiene la ecuación diferencial que refleja la dinámica del sistema eléctrico presentado:
![d2v(t) dv(t) u (t) = R1R2C1C2 -----+ [R1C1 +R1C2 + R2C2 ]-----+ v(t) dt dt](/file.php/83/problemas/modelo_circuito/ej3_html/ej311x.png)
Y finalmente, aplicando la transformada de Laplace a la ecuación anterior, considerando condiciones iniciales nulas, y despejando se obtiene la función de transferencia del sistema:
![V(s)= ------------------1------------------ U(s) R1R2C1C2s2 + [R1C1 + R1C2 + R2C2 ]s + 1](/file.php/83/problemas/modelo_circuito/ej3_html/ej312x.png)
Como se
puede comprobar, esta expresión obtenida no es el producto de las
funciones de transferencia de los dos circuitos sencillos.
Efectivamente, si así lo hiciéramos el término de la potencia de s sería ![[R1C1 + R2C2]](/file.php/83/problemas/modelo_circuito/ej3_html/ej313x.png) , faltando un término. Vamos a
buscar una explicación a esta aparente contradicción.
, faltando un término. Vamos a
buscar una explicación a esta aparente contradicción.
En realidad, el considerar que la función de transferencia de los dos circuitos en serie es el producto de las de cada uno de ellos por separado puede venir de considerarlos como circuitos aislados, tal y como se observa en la siguiente figura:
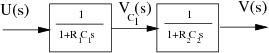
Sin embargo esto es erróneo, dado que si el circuito analizado se pudiera separar como se ha hecho en el diagrama de bloques, esto supondría que el segundo circuito no influye sobre el primero, y esto no es cierto. La flecha que “une” los sistemas 1 y 2 es unidireccional, esto es, la salida del sistema 1 VC1(t) influye sobre el segundo sistema (es su entrada), pero lo que pase en éste no afecta en el primero. En definitiva, a no ser que existiera una etapa que aisle los dos circuitos es erróneo obtener la función de transferencia del sistema completo como producto de las funciones de transferencia de los sistemas individuales.