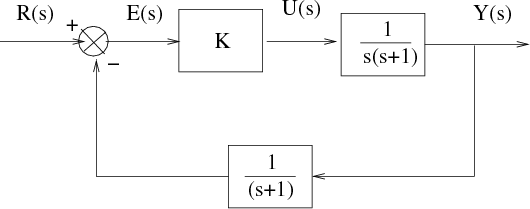
Obtener el valor de la salida en estacionario para el sistema de la figura, en función de la ganancia proporcional K , si se aplica la señal r(t) = 1 + t.

¿Que cambia si H(s) = 1∕(s + 2) ? (Responder sin realizar cálculos)

Solución:

Para empezar se debe asegurar la estabilidad en lazo cerrado. Para eso se utiliza el criterio de Routh-Hurwitz, aplicado a la ecuación característica del sistema:

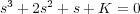
Todos los coeficientes deben ser positivos y por tanto, K > 0. Por otro lado, la tabla de Routh-Hurwitz es

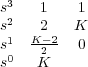
Todos los elementos de la primera columna deben de ser positivos y por tanto, el rango 0 < K < 2 define los límites de estabilidad. Dentro de este rango, se puede aplicar la propiedad de linealidad para la entrada considerada. Así es suficiente calcular el error estacionario ante entrada escalón y rampa, y para conocer la salida en estacionario sumarlo.

Para empezar, al ser la realimentación de ganancia unitaria (H(0)=1) y el sistema de tipo uno, el error en el permanente ante entrada escalón es nulo. Para la entrada rampa se puede utilizar la constante de error k_v o directamente la expresión siguiente

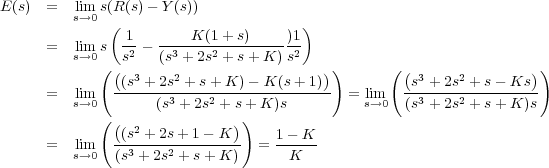
E (s) = sli→m0 s(R( (s) - Y (s)) ) -1 ----K-(1+-s)----)1 = sli→m0 s s2 - (s3 + 2s2 + s+ K )s2 (( 3 2 )) ( ( 3 2 )) = lim -(s-+-2s-+-s+-K-)--K-(s+-1)- = lim -s-+-2s-+-s--Ks-- s→0 (s3 + 2s2 + s+ K )s s→0 (s3 + 2s2 + s+ K )s (((s2 + 2s+ 1 - K)) = lim --3----2-------- = 1--K-- s→0 (s + 2s + s + K) K

Por tanto, y_∞ = r_∞- e_∞ = 1 + t -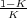 1-KK- .

Si se cambia la función de transferencia en la realimentación a H(s) = 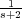s1+2 , su ganancia dejará de ser unitaria. De esta forma, la señal de error en el permanente se mantiene nula, pero el error (r_∞- y_∞) no, ya que, siendo la señal de error r_∞ - 2y_∞ finita, el error r_∞ - y_∞ no lo será, puesto que la entrada tiene un señal rampa que tiende a infinito.