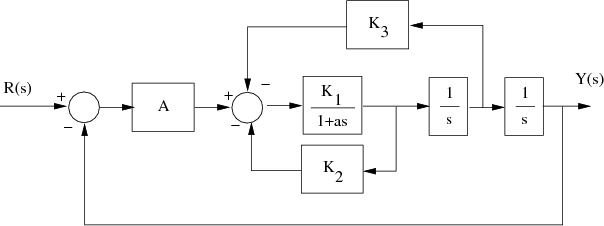
Obtener la función de transferencia del sistema de la Figura, y calcular los valores del parámetro A para los cuales el sistema es estable.

Vamos a ir reduciendo el diagrama de bloques del sistema para obtener la fiunción de transferencia 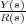Y(s) R(s)

del mismo. En un primer paso podemos reducir el lazo cerrado formado por los bloques 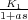1K+1as

y K₂ de tal modo que:

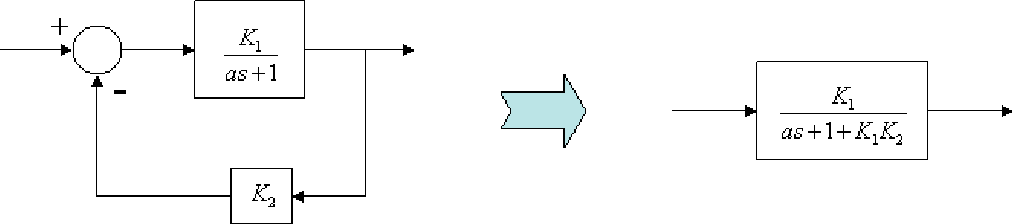
Este bloque queda en cascada con uno de los bloques 1 s

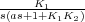, por lo que dichos bloques pueden ser reducidos a uno solo de función de transferencia -----K1---- s(as+1+K1K2)

. Después de estas operaciones el diagrama de bloques del sistema es:

El lazo cerrado formado por los bloques 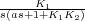-----K1---- s(as+1+K1K2)

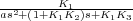y K₃ puede ser sustituido por un bloque de función de transferencia -------K1-------- as2+(1+K1K2)s+K1K3

en la cadena directa, siguiendo el mismo procedimento que el comentado en el primer paso. Este bloque está en cascada con lo bloques A y 1 s

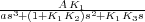, por lo que pueden ser sustituidos los tres bloques por uno solo de función de transferencia --------AK1-------- as3+(1+K1K2 )s2+K1K3s

. De esta forma se obtiene el diagrama de bloques de un sistema en lazo cerrado con realimentación unitaria, mostrado en la siguiente figura:

A partir de este esquema se obtiene la función de transferencia del sistema completo, resultando:

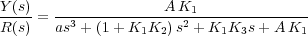
Y-(s) --------------A-K1-------------- R (s) = as3 + (1 +K1K2 )s2 +K1K3s + AK1

A continuación estudiamos la estabilidad del sistema respecto del parámetro A. Para ello, aplicamos el criterio de Routh-Hurwitz al polinomio denominador de la función de transferencia, es decir, a D(s) = as³ + 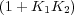(1+ K1K2 )

s² + K₁K₃s + AK₁. La tabla de Routh de dicho polinomio es:

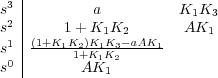
3 | s2 | a K1K3 s |(1+K11K+2)KK11KK23-aAK1 AK1 s1 |-----1+K1K2------ s0 AK1

Observando las expresiones de la primera columna a la derecha de la línea en dicha tabla, se obtienen las siguientes condiciones necesarias y suficientes para la estabilidad del sistema.

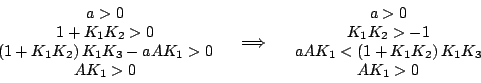
a > 0 a > 0 1+ K K > 0 K K > - 1 { (1 + K K )K1K 2- aAK > 0 =⇒ { aAK < 1(1 +2K K )K K 1 2AK1 >30 1 1 AK >10 2 1 3 1 1

Notad que en la tercera de las condiciones no se simplifica la ganancia K₁ ya que dicha simplificación lleva consigo un cambio del operador relacional < por > si la ganancia K₁ es negativa. Se pueden dar dos casos:

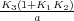Caso 1: Si K₁ > 0 entonces el sistema es estable si 0 < A < . Notad que K₃ ha de ser positivo en este caso para que existan valores de A que garanticen la estabilidad del sistema.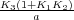
Caso 2: Si K₁ < 0 entonces el sistema es estable si < A < 0. Notad que K₃ ha de ser negativo en este caso para que existan valores de A que garanticen la estabilidad del sistema.

Notad que el caso K₁ = 0 no tiene sentido ya que en tal situación se anula uno de los bloques de la cadena directa del sistema y la salida del mismo es nula para cualquier entrada que se le aplique al sistema.