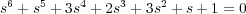
Estudiar la estabilidad de un sistema cuya ecuación característica es la dada y obtener así mismo sus raíces:
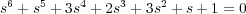
Solución:
Haremos uso del criterio de Routh-Hurwitz para estudiar la estabilidad del sistema. Para ello, construimos la tabla de Routh correspondiente al polinomio característico del sistema, es decir, del polinomio D(s) = s6 + s5 + 3s4 + 2s3 + 3s2 + s + 1. Dicha tabla es :
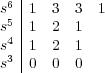
Se observa que se obtiene
una fila de ceros. Para continuar con la construcción de la tabla se
sustituye dicha fila por los coeficientes del polinomio obtenido al
derivar respecto de s el polinomio
auxiliar A1(s) = s4 + 2s2 + 1. Este
polinomio se obtiene con los coeficientes de la fila situada justo
encima de la fila de ceros en dicha tabla y su orden es el
correspondiente a dicha fila. Además, las potencias de los términos de
dicho polinomio auxiliar son alternas. En este caso sólo contiene
potencias pares. Derivando el polinomio auxiliar se obtiene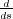 
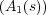= 4s3 + 4s y los coeficientes 4 y 4 son usados en
lugar de los ceros de la fila para continuar con la construcción de la
tabla. Entonces,
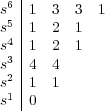
Vuelve a aparecer una
fila de ceros. Siguiendo el mismo procedimiento que en el caso
anterior, el polinomio auxiliar ahora es A2(s) = s2 + 1 y su
derivada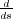 
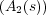= 2s.
Entonces, el coeficiente 2 es utilizado en
lugar del cero en la fila y se continua la construcción de la tabla.
Entonces,
Una vez construida la
tabla se aplica el criterio de Routh-Hurwitz para estudiar la
estabilidad del sistema. Para ello hay que fijarse en la lista de
números de la primera columna a la derecha de la línea continua de la
tabla, reemplazando en dicha lista los números de las filas de s3 y de
s1,
es decir el 4 y el 2, por ceros, que son realmente los coeficientes
que se obtienen en la construcción de la tabla. Los números 4 y el 2 son
necesarios para poder completar la construcción de la tabla pero no
deben ser usados para la aplicación del criterio de estabilidad de
Routh-Hurwitz. Por tanto, la lista de números es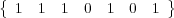 
.
Al recorrer dicha lista se observa que hay dos pasos de positivo a cero
y otros dos de cero a positivo. Por tanto, el sistema tiene dos parejas
de polos complejos conjugados sobre el eje imaginario y los otros dos
polos están en el semiplano izquierdo del plano complejo.
Los polos del sistema , o
raíces del polinomio característico D(s) = s6 + s5 + 3s4 + 2s3 + 3s2 + s + 1, se pueden
obtener de la siguiente forma. Ya que las raíces de los polinomios
auxiliares que se han usado para construir la tabla de Routh también
son raíces de D(s) entonces 4 de dichas raíces son aquellas de
A1(s) = s4 + 2s2 + 1 =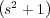 
2, es decir:
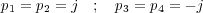
siendo j la unidad imaginaria. Las otras dos raíces son las del polinomio cociente de la división de D(s) entre A1(s), es decir,
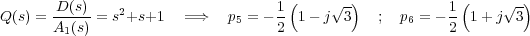
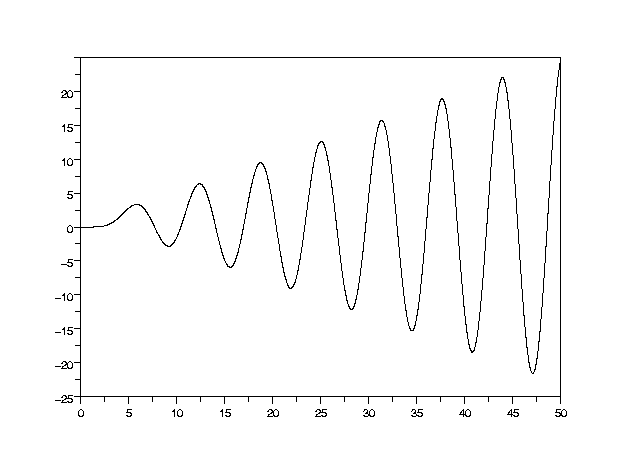
En este caso se ha podido obtener los valores de las 6 raíces del polinomio D(s), cuatro de las cuales son imaginarias puras. En consecuencia, podría deducirse que el sistema es críticamente estable (2 raíces estables y 4 en el eje imaginario). Sin embargo no es así, si D(s) fuera el polinomio denominador de un sistema , éste sería inestable. La razón es que los polos en el eje imaginario hacen el sistema críticamente estable sin son simples, si no lo hacen inestable. Efectivamente, si obtenemos la respuesta del sistema G(s)=1/D(s) ante entrada escalón unitario se obtiene la señal de la figura:
