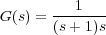
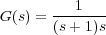
Solución. Para empezar, el diagrama de bloques del sistema considerado es:
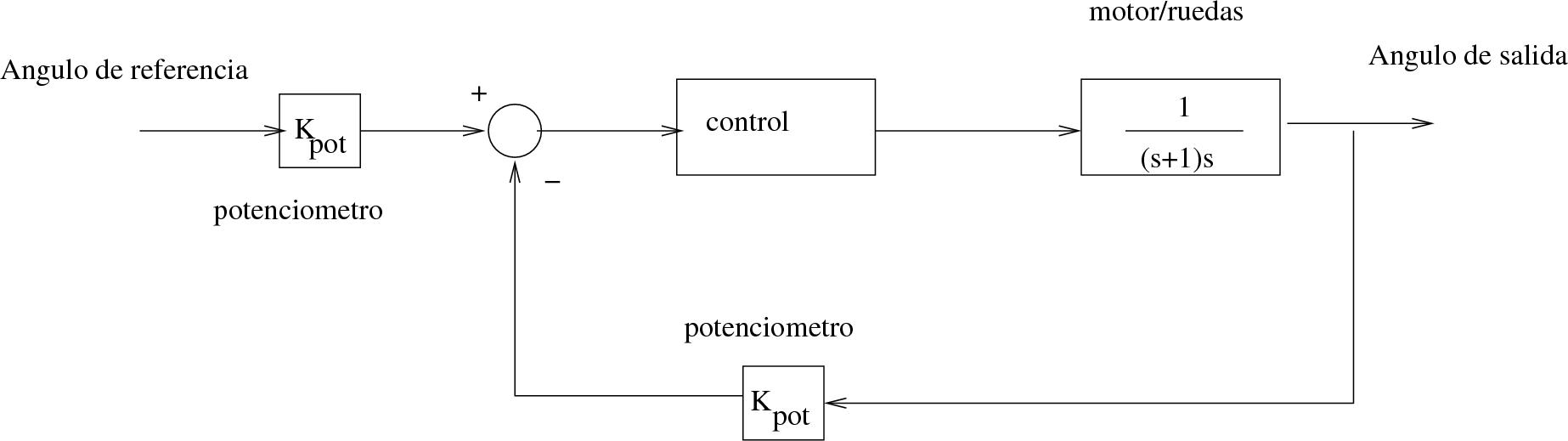
Por tanto, la función de transferencia del sistema en lazo abierto es
Gabierto = 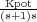 . Para elegir los polos dominantes se puede pensar que un
coeficiente de amortiguamiento en el rango 0.6-0.8 puede ser interesante
para mantener las oscilaciones bajas. Sin embargo, teniendo en cuenta el
cero que añade el controlador PD (aunque aún no se sepa donde estará),
puede ser interesante amortiguar aún más el sistema desde el principio. Por
ello, se elige un valor inicial δ = 0.9, recordando que un diseño completo
puede pasar por varias fases de prueba y error (aunque en este texto solo se
describe el primer paso). Por tanto, recordando el tiempo de establecimiento
deseado
. Para elegir los polos dominantes se puede pensar que un
coeficiente de amortiguamiento en el rango 0.6-0.8 puede ser interesante
para mantener las oscilaciones bajas. Sin embargo, teniendo en cuenta el
cero que añade el controlador PD (aunque aún no se sepa donde estará),
puede ser interesante amortiguar aún más el sistema desde el principio. Por
ello, se elige un valor inicial δ = 0.9, recordando que un diseño completo
puede pasar por varias fases de prueba y error (aunque en este texto solo se
describe el primer paso). Por tanto, recordando el tiempo de establecimiento
deseado
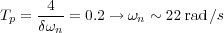
y los polos dominantes deseados son s1,2 = -20 ± 9.7j. Planteando la condición del argumento
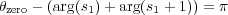
se obtiene que la fase que tiene que proporcionar el cero del PD para que los polos dominantes pertenezcan al lugar de las raices es θzero = 2.22rad. Así,
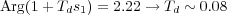
Esto es, el cero del PD esta situado en el punto -12.6. Para añadir la parte integral del controlador, se elige la posición del cero del PI de forma que se situa 10 veces más cerca del eje imaginario que los polos “dominantes” deseados (¿son realmente dominantes? Hay que comparar con la posición del cero de la parte PD introducida). Por tanto,
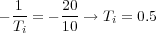
Para terminar el diseño falta obtener la constante proporcional necesaria para que los polos deseados sean realmente polos en lazo cerrado. Este valor se obtiene utilizando el criterio del módulo
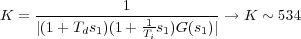
Una vez terminado el diseño se observa que el cero del controlador PD esta (bastante) más cerca del eje imaginario que los polos “dominantes” y por tanto, se puede esperar una sobreelongación importante en la salida (más o menos el %16). Para resolver este problema se puede recurrir al método de prueba y error. Hay dos posibilidades a estudiar que se dejan como ejercicio: aumentar el coeficiente de amortiguamiento inicial o bajar la velocidad (aumentando el tiempo de establecimeinto pedido).
En cuanto al error en permanente, conocido que el sistema es estable, se puede calcular mediante Kv
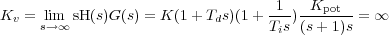
Esto es, el error en permanente ante entrada rampa es nulo (se debe recordar que, en este caso siendo la realimentación unitaria, el valor del error en estacionario y la señal de error en estacionario coinciden). Esto era conocido a priori ya que el sistema es de tipo 2, gracias al PI. Sin embargo, considerando Kpot = 2 cambian dos cosas: la ganancia de lazo abierto y que el error en estacionario y la señal de error en estacionario no coinciden, ya que la ganancia de realimentación no es unitaria. El primer problema se soluciona cambiando la ganancia del control proporcional K′ = K∕Kpot. En el segundo caso, como la referencia queda multiplicada también por Kpot (r′ = Kpotr), el error en estacionario ante entrada rampa tampoco cambia (utilizando K′):
| e′∞ | = limt→∞r - y = lims→0 sR(s)(1 - K′Kpot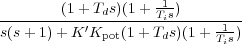 ) ) | ||
= lims→0 sR(s)(1 - K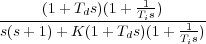 ) = e∞ ) = e∞ |