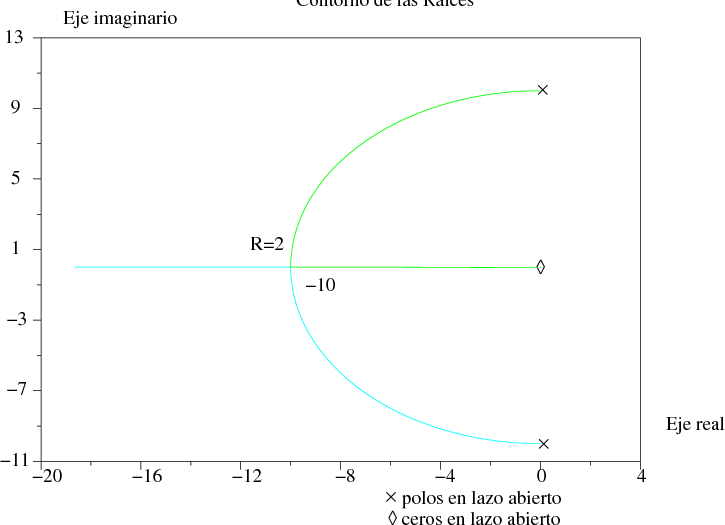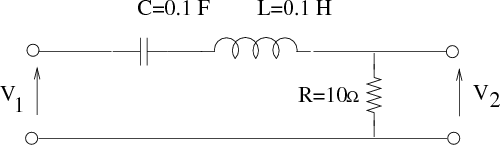
Considerando el circuito de la siguiente figura:

 

PIC

 

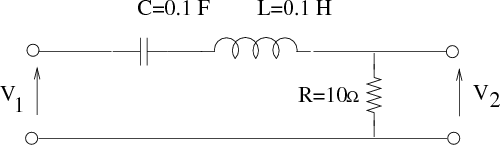
Solución:

La impedancia equivalente es :

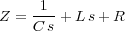
1 Z = --- +L s+ R C s

El voltaje de entrada es V1 = Z i y el de salida V2 = Ri. Por tanto, la función de transferencia pedida será:

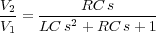
V2 = -----RC--s----- V1 LC s2 + RC s + 1

Obteniendo la salida Y (s) en el dominio de Laplace, cuando V1(s) = 1/s, se puede proceder a obtener y(t) a tráves del cálculo de la antitransformada de Laplace:

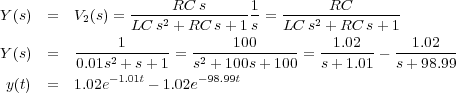
Y (s) = V2(s) = -----RC-s------1= -----RC-------- LC s2 + RC s+ 1 s LC s2 + RC s+ 1 Y (s) = -----1------= -----100------= --1.02-- - --1.02--- 0.01s2 + s+ 1 s2 + 100s +100 s + 1.01 s+ 98.99 y(t) = 1.02e-1.01t - 1.02e-98.99t

Aproximadamente, la salida del sistema es similar a la respuesta impulsional de un sistema de primer orden, ya que una de la exponenciales cae muy rápidamente a cero:

PIC

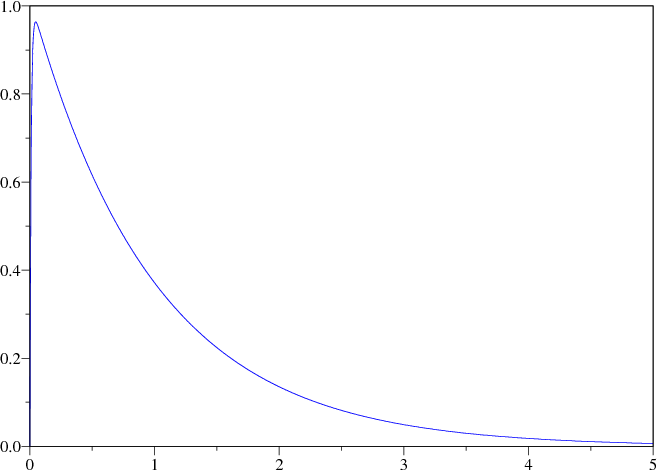
En el permanente la señal de salida es nula (se tiene un condensador con un voltaje aplicado constante). Para obtener este resultado se puede aplicar el teorema del valor final

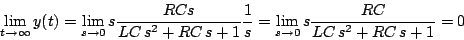
RCs 1 RC tli→m∞ y(t) = lsim→0s---2----------- = lsim→0s ----2---------0 LC s + RC s+ 1s LC s + RC s+ 1

La ecuación característica del sistema a estudiar es

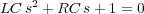
LC s2 + RC s +1 = 0

se puede reescribir de la siguiente forma

 

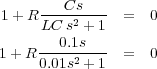
Cs 1 +R LC-s2 +-1 = 0 0.1s 1+ R ----2---- = 0 0.01s + 1

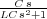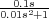Así, la función de transferencia auxiliar para obtener el contorno de las raíces en función de R es TF = --Cs-- LCs2+1 = -0.1s--- 0.01s2+1.

Cálculo del contorno de las raíces

- Dos ramas, una acaba en el cero del origen y la otra a través del eje real en -∞ (una única asíntota)

- Ángulo de salida de los polos: planteando la condición de fase para el polo (s = 10j)

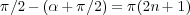
π∕2- (α + π∕2) = π(2n+ 1)

Para n = 0, el ángulo de salida es α = π. Por simetría, para el polo s = -10j el ángulo de salida también es π.

- El ángulo de llegada al cero es evidente del comportamiento en el eje real.

- Posibles puntos de dispersión, soluciones de la ecuación

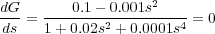
dG- ---0.1--0.001s2---- ds = 1+ 0.02s2 + 0.0001s4 = 0

Así el punto s = -10 es punto encuentro (el punto s = 10 no pertenece al contorno de las raíces).

- Aplicando Routh-Hurwitz a la ecuación característica 0.01s2 + R0.1s + 1 = 0 para R > 0, se puede estudiar la estabilidad y los cruces del eje. Tabla de Routh-Hurwitz

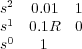
2 s1 0.01 1 s0 0.1R 0 s 1

Por tanto, si R > 0 el sistema es estable siempre (es un circuito pasivo).

PIC

Analizando el contorno de las raíces, está claro que el sistema es siempre estable. Para valores pequeños de R el sistema es muy oscilatorio (subamortiguado), aumentando la amortiguación según aumenta el valor de la resistencia. Al disminuir las oscilaciones también se reduce el tiempo de establecimiento. A partir del valor R = 2 los polos del sistema son reales (punto de encuentro), desapareciendo el caracter oscilatorio de forma definitiva. A partir de ese punto, si se aumenta el valor de la resistencia un polo se acerca por el eje real al origen, siendo el dominante y el otro se aleja. De esta forma la dinámica del sistema se ralentiza según aumenta la resistencia. Sin embargo, hay que recordar el cero en origen que posee el sistema en lazo cerrado (al igual que la función auxiliar, pero esto es solo una casualidad). Este cero muy dominante genera un rebose muy importante.