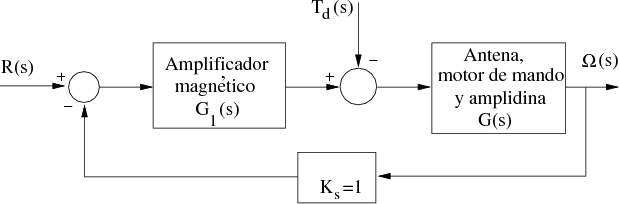
Considérese el sistema de control de velocidad de la figura siguiente, compuesto de una antena parabólica direccionable mediante la acción de un amplificador magnético que genera la señal de control que actúa sobre la antena.

Como se puede observar en la figura, se trata de un problema de seguimiento, dado que la variable que se pretende controlar es la velocidad de giro de la antena (en lugar de la posición de la misma).

La acción que realiza el viento sobre la antena se considera como una perturbación (T_d(t)) que actúa sobre la señal de control y el resto de bloques se pueden aproximar por:

1. Se quiere diseñar el sistema para que la acción del viento sea despreciable sobre la posición de la antena. Se considera que la acción del viento se puede simplificar por una señal constante T_d(t)=0,2 voltios.
   Determínese el valor de la constante K_a del amplificador  con el objeto de mantener el error estacionario por debajo de 0,083 rpm cuando la entrada r(t) es 9,55 rpm.
2. Determínese el error estacionario del sistema diseñado sin realimentación (K_s=0) ante la misma perturbación (T_d(s) =0,2 voltios) y entrada r(t)=9,55 rpm.
3. Comparar y discutir los errores que presenta el sistema en los dos casos anteriores.

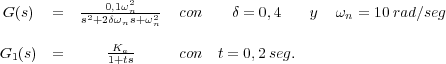
Solución:

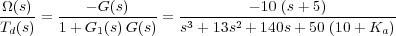
Por otro lado, la función de transferencia que relaciona la velocidad de giro de la antena con la señal de referencia R(s) es:

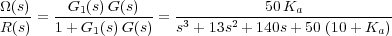
Antes de proceder al cálculo del valor de la ganancia K_a del amplificador que garantiza el comportamiento en el permanente que se pide, estudiemos el rango de valores de dicha ganancia para el cual el sistema es estable. Para ello aplicamos el criterio de Routh-Hurwitz al polinomio característico del sistema, esto es al polinomio D(s)=s³+13s²+140s+50. La tabla de Routh correspondiente es :

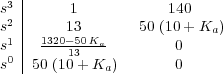
La condición necesaria y suficiente para que el sistema sea estable es:  

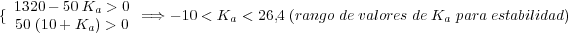
Para este rango de valores de K_a tiene sentido el estudio del régimen permanente.

El error del sistema, Er(s)=R(s)-Ω(s), que en este caso coincide con la señal de error al ser la realimentación unitaria, depende tanto de la señal de referencia como de la señal de perturbación. Es decir,

donde _Td(s)=0 denota la función de transferencia que relaciona el error con la señal de referencia cuando la perturbación es nula y _R(s)=0 la función de transferencia que relaciona el error con la señal de perturbación cuando la referencia es nula. Haciendo cálculos se obtiene:

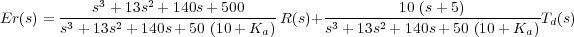
El error en régimen estacionario ante una entrada r(t)=9,55 rpm=1 rad/seg y una perturbación T_d(t)=0,2 V es:

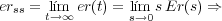
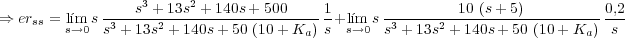
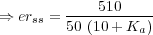
Esta expresión para el error es válida para valores de K_a que hacen que la función Er(s) sea analítica en el semiplano derecho del plano complejo y, por tanto, sea aplicable el teorema del valor final de la transformada de Laplace, es decir, lim_t→∞er(t) = lim_s→0sEr(s) . Dicho rango de valores de K_a es el mismo para el cual el sistema es estable, es decir, -10 < K_a < 26,4. De la expresión para el error, er_ss = 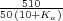, se deduce que cuanto mayor sea la ganancia K_a del amplificador mejor es la precisión del sistema de seguimiento. En este sentido, el mínimo error de seguimiento que se puede obtener para las entradas de referencia y perturbación consideradas es er_ss=0,28 rad/seg=2,67 rpm, cuando el valor de la ganancia del amplificador está ajustado a K_a=26,4. Para que el error fuera inferior a 0,083 rpm, como demanda el enunciado del problema, haría falta un valor de K_a para el cual el sistema no es estable. Por tanto, no existe un valor para la ganancia K_a que haga el error inferior a 0,083 rpm para dichas entradas de referencia y perturbación.

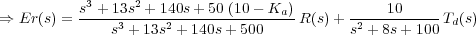
Aplicando el teorema del valor final de la transformada de Laplace y considerando las mismas señales de entrada y perturbación que en el apartado (i) se obtiene:

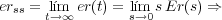
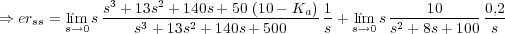
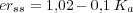
Considerando el valor K_a=26.4, para el cual se obtiene la mejor precisión del sistema en lazo cerrado, el error del sistema en lazo abierto es er_ss=-1,62 rad/seg. Esto quiere decir que si la señal de referencia es de r(t)=1 rad/seg la salida en el permanente es ω(t)=2,62 rad/seg. Es decir, la antena se mueve a una velocidad que es un 162% más rápida que la velocidad de referencia.

Observación final

Las resoluciones de todos los ejercicios de esta asignatura están pensadas que sean "sobre el papel", esto es, sin ayuda informática. Sin embargo, como se presenta el programa Scilab como ayuda para el estudio conviene hacer un comentario a la solución presentada de este ejercicio.

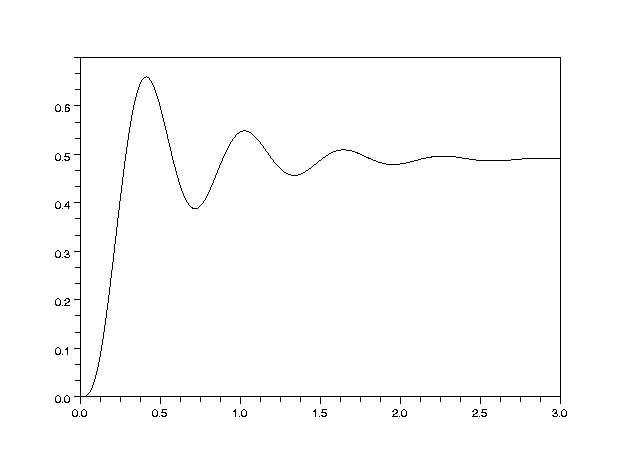
En principio cabe pensar que la resolución ha sido correcta y que el mejor valor del parámetro K_a con vistas a mejorar la precisión del sistema es 26.4, que corresponde al valor mayor dentro del rango que hace que el comportamiento en lazo cerrado sea estable. Vamos a utilizar el programa Scilab para obtener la señal de salida del sistema (velocidad de seguimiento de la antena):

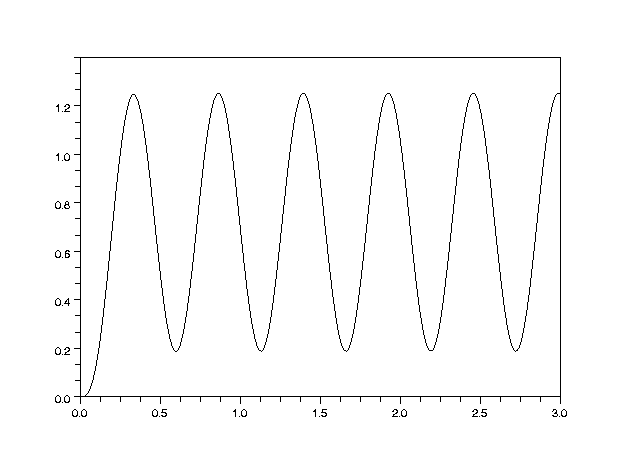
Como se puede observar, la velocidad de seguimiento es oscilatoria. Y aunque la media de la oscilación corresponde al valor de error mínimo calculado, se puede decir que el control no es muy bueno. ¿Qué está pasando?, ¿finalmente no es buena la elección del parámetro K_a?.

La razón de esta contradicción hay que buscarla en la elección del parámetro. Efectivamente, el comportamiento del sistema para un valor de K_a cercano a la estabilidad crítica, es apreciablemente oscilatorio. Por lo tanto, aunque matemáticamente es la mejor elección en cuanto a precisión, no es así en cuanto a comportamiento general del sistema realimentado, y habría que buscar un compromiso entre precisión y comportamiento. Por ejemplo, en la siguiente figura se muestra la salida del sistema con una elección de K_a=10. Y aunque el error es superior (er_ss=0,51 rad/seg=4,87 rpm) al anterior, el resultado final podría considerarse mejor.