Práctica: Análisis y Diseño de un sistema de control de posición de una bola metálica mediante levitación magnética

En los últimos tiempos se ha comenzado a utilizar la levitación magnética para suspender en el aire sin ningún contacto físico con soporte alguno diferentes elementos móviles como pueden ser el rotor de un motor o de una máquina herramienta, o más conocido un tren de alta velocidad.

Las ventajas son indudables, entre las que se pueden destacar la total ausencia de rozamiento entre el elemento móvil y su soporte. Ahora bien, la tecnología necesaria para un correcto funcionamiento es también mucho más compleja que la utilizada para los sistemas tradicionales (mediante cojinetes).

Modelización

Figura 1:

Sistema simplificado de levitación magnética de una bola metálica

En esta práctica se va a estudiar un modelo reducido (Figura 1) que permitirá comprender algunas de las problemáticas presentes en los sistemas reales.

El sistema consiste en un electroimán (bobina con nucleo de hierro) que al aplicarle una corriente ejerce una fuerza ascendente sobre la bola que permite contrarrestar la fuerza de la gravedad y hacer levitar la bola metálica. Dicha fuerza es proporcional al cuadrado de la intensidad que circula por la bobina, e inversamente proporcional al cuadrado de la distancia (se considera positivo en sentido descendente) que separa la bola levitada de la misma:

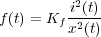i2(t) f(t) = Kf x2(t)-

(1)

Aplicando la ley de Newton al sistema mecánico se tiene que la ecuación que define su dinámica es:

d2x(t) i2(t) m -dt2--= mg - f(t) = mg - Kfx2(t)

(2)

Figura 2:

Esquema simplificado de la bobina del electroimán

Por otra parte la dinámica de la bobina se puede simplificar por un circuito RL (Figura 2), que aplicando las leyes de Kirchoff permiten obtener la ecuación diferencial:

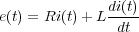di(t) e(t) = Ri(t)+ L-dt

(3)

donde e(t) e i(t) son, respectivamente, la tensión aplicada en los bornes de la bobina y la intensidad que circula por la misma.

Linealización

En definitiva las dos ecuaciones anteriores (2) y (3 ) representan la dinámica del sistema completo. Pero como se ha mencionado anteriormente será necesario linealizar la primera de ellas.

La linealización de la relación (1) supone escoger un punto de equilibrio a partir del cual va a funcionar el sistema, esto es, se supone una intensidad i(t) = i₀ que permite ejercer a la bobina una fuerza f(t) = f₀ = mg tal que mantenga la bola suspendida a una distancia x(t) = x₀. La relación entre todas las señales anteriores se puede concluir de la ecuación diferencial mecánico-magnética (2):

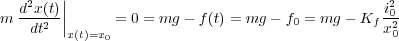2 || 2 m d-x(t)|| = 0 = mg - f(t) = mg - f0 = mg - Kf-i02 dt2 x(t)=x0 x0

(4)

Si a partir de este punto de equilibrio se produce un pequeño incremento en la intensidad que recorre la bobina, se produce en consecuencia pequeños incrementos tanto de la fuerza ejercida por el electroimán como en la posición de la bola:

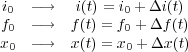i0 - → i(t) = i0 + Δi(t) f0 - → f (t) = f0 + Δf (t) x0 - → x(t) = x0 +Δx (t)

(5)

De esta forma la relación no lineal (1 ), haciendo un desarrollo en serie de Taylor y despreciando los términos que supongan al menos un incremento al cuadrado (si los incrementos son grandes no será válida la linealización) quedará:

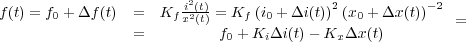f (t) = f + Δf (t) = K -i2(t)= K (i + Δi(t))2(x + Δx (t))-2 0 fx2(t) f 0 0 = = f0 + KiΔi (t)- Kx Δx(t)

(6)

y operando se obtiene una relación lineal entre los incrementos de las variables del sistema (Δi(t), Δf(t) y Δx(t)):

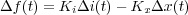Δf(t) = KiΔi(t)- Kx Δx(t)

(7)

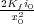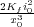con K_i = 2Kf2i0- x0 y K_x = 2Kf3i20 x0 .

Sistema en lazo abierto

Utilizando la relación lineal anterior en la ecuación diferencial de la mecánica del sistema (2 ) se tiene:

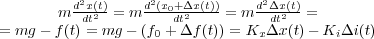d2x(t) d2(x0+Δx(t)) d2Δx(t) m dt2 = m dt2 = m dt2 = = mg - f(t) = mg - (f0 +Δf (t)) = KxΔx (t) - Ki Δi(t)

(8)

Quedando la ecuación diferencial que representa la dinámica del sistema a partir del punto de equilibrio (i0, x0, f0) :

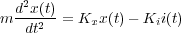d2x(t) m ---2--= Kxx(t)- Kii(t) dt

(9)

siendo las variables x(t) e i(t) los incrementos del desplazamiento de la bola y el de la intensidad que recorre la bobina desde sus valores en el punto de equilibrio, respectivamente.

Aplicando la transformada de Laplace a la ecuación anterior y suponiendo las condiciones iniciales nulas se obtiene la función de transferencia que relaciona las variables intensidad y desplazamiento:

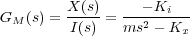X (s) - K GM (s) = -----= --2--i--- I(s) ms - Kx

(10)

Por otra parte la función de transferencia del subsistema eléctrico se obtiene a partir de sus ecuación diferencial (3 ):

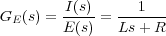I(s) 1 GE (s) = E(s) = Ls+-R-

(11)

quedando el sistema completo reflejado en el diagrama de bloques de la Figura 3 .

Figura 3:

Diagrama de bloques del sistema en lazo abierto

Cuestion1: Realizar el análisis del sistema en lazo abierto (Figura 3) resultante.

Control PD

A continuación se añade al sistema un control PD (proporcional-derivativo), quedando el esquema de control de la forma mostrada en la Figura 4 .

Figura 4:

Diagrama de bloques del sistema en lazo cerrado con control PD

Cuestión 2: Considerando que los valores de los parámetros del controlador son k_d = -3 y T_d = 0,02, analizar la respuesta del sistema en lazo cerrado ante una entrada escalón.

Cuestión 3: Manteniendo el valor de k_d = -3 obtener el contorno de las raíces del sistema con respecto a T_d. Razonar como se podría mejorar la respuesta del sistema apoyándose en este contorno de las raíces.

Cuestión 4: Manteniendo el valor de T_d = 0,02 obtener el lugar de las raíces del sistema con respecto a k_d. Razonar como se podría mejorar la respuesta del sistema apoyándose en este lugar de las raíces.

Cuestión 5: Obtener los valores para los parámetros del controlador PD para que la respuesta del sistema ante una entrada escalón cumpla las siguientes especificaciones: (1) Tiempo de establecimiento menor o igual a 5 segundos y (2) rebose porcentual menor o igual al 20 %.

Cuestión 6: Obtener los valores para los parámetros del controlador PID para que la respuesta del sistema ante una entrada escalón cumpla las siguientes especificaciones: (1) Tiempo de establecimiento menor o igual a 5 segundos y (2) rebose porcentual menor o igual al 20%.

Cuestión 7: Comparar los resultados de las cuestiones 5 y 6 de forma razonada, destacando las ventajas y desventajas obtenidas en cada caso.

Metodología de resolución

La práctica se llevará a cabo utilizando los contenidos del curso Automática utilizando el programa de libre distribución Scilab. Una breve descripción de comandos que se pueden utilizar se encuentra aqui. Para más información visitar la página web www.scilab.org.

Por otro lado, se puede comprobar mediante Scicos, utilizando el modelo no lineal, si el diseño realizado es válido para este modelo más realista.

Nota para la resolución de la cuestión 5: El diseño del control PD consistirá en obtener los valores de las constantes proporcional y derivativa del mismo, y para ello se va a utilizar el Lugar de las Raíces del sistema. Primeramente se deberá elegir una dinámica transitoria adecuada para el sistema, de tal forma que si se supone que la misma corresponde a un sistema de segundo orden (sin ceros) quedarán fijados los dos polos complejos conjugados en lazo cerrado (s_1,2). Y por lo tanto dichos polos deberán pertenecer al Lugar de las Raíces y por ello cumplir la condición de Argumento:

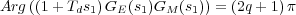Arg ((1+ Tds1)GE (s1)GM (s1)) = (2q+ 1)π

(12)

siendo s₁ = -δω_n + jω_d, con los parámetros δ y ω_n fijados al escoger la pareja de polos s_1,2 que determinan la dinámica dominante del sistema. Y de la ecuación anterior se puede obtener la constante derivativa. La otra constante del controlador se obtendrá mediante la condición del módulo:

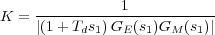1 K = |(1+-Tds1)GE-(s1)GM-(s1)|

(13)

Por último será necesario reajustar los valores obtenidos, dado que el sistema real no es de segundo orden. Observando los Lugares de las raíces para las constantes proporcional y derivativa (en este caso Contorno de las Raíces) se podrá deducir la forma de modificar dichos parámetros.

Datos: los valores de las diferentes constantes del sistema son:

$m = 200 gr. x0 = 5cm. R = 1Ω Kf = 1N.m ∕A2 L = 0,01H$