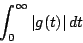Estabilidad. Criterio de Routh-Hurwitz

Se estudian una serie de definiciones de estabilidad de sistemas lineales mostrando la equivalencia entre ellas. Se profundiza en la utilización del criterio de Routh-Hurwitz, que es válido para el estudio de la estabilidad absoluta (el sistema es estable o no lo es) de sistemas lineales e invariantes en el tiempo.

5.1. Introducción       Ir al Indice

La estabilidad es uno de los requisitos básicos para cualquier sistema de control diseñado para satisfacer unas especificaciones deseadas. Esto es, todo sistema de control, aparte de otras características, ha de ser siempre estable por lo que el estudio de la estabilidad constituye una parte importante tanto del diseño como del análisis de los sistemas de control.

La estabilidad de los sistemas se puede estudiar desde dos enfoques diferentes: la estabilidad absoluta y la estabilidad relativa. La estabilidad absoluta es de naturaleza cualitativa. Se trata de responder simplemente sí o no a la pregunta de si el sistema es estable.

La segunda cuestión, el problema de la estabilidad relativa, es de naturaleza cuantitativa: se trata de averiguar en qué grado el sistema es estable. Aunque esta cuestión es más difícil de resolver que la primera su solución da, evidentemente, más información sobre el sistema y es un puente entre la información dada por el estudio de la estabilidad absoluta y la dada por el estudio de la respuesta temporal total del sistema. El estudio de la estabilidad relativa de un sistema de control supone muchas veces su análisis en profundidad, y con ello obtener información no solo de su estabilidad sino del comportamiento temporal del mismo ante diversas señales de entrada.

En este capítulo se va a definir en primer lugar el concepto general de estabilidad, pasando posteriormente al estudio de la estabilidad absoluta. El problema de la estabilidad relativa será tratado brevemente, y de una forma descriptiva, en los siguientes capítulos, dejando su estudio en profundidad para la asignatura Sistemas Continuos de Control.

5.2. Definiciones de Estabilidad       Ir al Indice

Como se verá a continuación, no existe una única definición de estabilidad y, aún cuando exista una clara relación entre las diferentes definiciones, éstas no son completamente equivalentes. En concreto, se puede decir que tres definiciones son las más comúnmente utilizadas. Las tres definiciones son de igual importancia y veremos como, bajo ciertas condiciones, las tres son equivalentes.

Definición 1:

Un sistema es estable si la salida permanece acotada para una entrada acotada .

Definición 2:

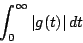Un sistema lineal es estable si la respuesta impulso o función impulsional es absolutamente integrable en el rango infinito, esto es, si es finita.

Definición 3:

Un sistema lineal es estable si todos los polos de su función de transferencia están en el semiplano izquierdo del plano s.

La definición 1 recibe el nombre de estabilidad BIBO (siglas de Bounded Input Bounded Output). Nótese que las dos primeras definiciones hacen referencia a la respuesta temporal del sistema (dominio temporal), mientras que la tercera se refiere a las características del modelo matemático del mismo (dominio frecuencial).

Para el tipo de sistemas con los que se va a trabajar normalmente en la Ingeniería de Control se puede dar otra definición de estabilidad equivalente a la definición 2.

Definición 2.1:

Un sistema lineal es estable si su función de peso decae a cero cuando t →∞ (función peso es equivalente a respuesta impulsional), es decir, si lim_t→∞g(t) = 0.

Y finalmente, puesto que los polos de la función de transferencia de un sistema lineal son los valores propios de la matriz A de las ecuaciones de estado del mismo, podemos dar una definición equivalente a la 3 para el caso en que el sistema esté descrito en el espacio de estados.

Definición 3.1:

Un sistema lineal es estable si todos los valores propios de la matriz A están en el semiplano izquierdo.

Decir que esta última definición de estabilidad quedará totalmente explicada y entendida cuando se estudie la representación interna de los sistemas de control (asignatura Sistemas Continuos de Control).

Es de resaltar que según la definición 3 el estudio de la estabilidad de un sistema se reduce simplemente a estudiar la localización de los polos de la función de transferencia dentro del plano s. Este problema es el que va a ser abordado en la siguiente sección de este tema.

5.3. Criterio de Routh-Hurwitz       Ir al Indice

Según la definición 3 de estabilidad vista anteriormente, al ser la función de transferencia de un sistema un cociente de polinomios en s, la estabilidad BIBO (entrada acotada-salida acotada) del sistema está completamente determinada por los polos de G(s). En este sentido, si todos ellos tienen partes reales negativas entonces el sistema es estable BIBO.

Se dice que un polinomio es de Hurwitz si todas sus raíces tienen partes reales negativas. Por tanto, el problema de la estabilidad se reduce a saber si el polinomio denominador de la función de transferencia es de Hurwitz o no. Un método directo sería resolver el polinomio, pero si el grado de éste es elevado, esta tarea es altamente costosa. Por otra parte, el conocimiento de las ubicaciones exactas de las raíces no es necesario en cuanto al estudio de la estabilidad absoluta se refiere. En esta sección vamos a estudiar un criterio que permite determinar si un polinomio es de Hurwitz o no, sin necesidad de obtener las raíces del polinomio. Consideremos el siguiente polinomio:

en donde todos los coeficientes son números reales. En primer lugar, se puede demostrar que con a₀>0 si alguno de sus coeficientes es negativo o nulo, el polinomio no es de Hurwitz. Esta condición solo es necesaria, y puede ocurrir que un polinomio con todos sus coeficientes positivos no sea de Hurwitz. La condición necesaria y suficiente para que un polinomio sea de Hurwitz la proporciona el llamado Criterio de Routh-Hurwitz.

Para la aplicación de dicho criterio se sigue el siguiente procedimiento. A partir del polinomio D(s) se forman dos polinomios:

A continuación, se construye la tabla de Routh:

Las dos primeras filas de la tabla están formadas por los coeficientes de los polinomios D₁(s) y D₂(s), respectivamente. Para obtener el resto de los coeficientes de la tabla  hay que hacer un cálculo similar al de un determinante (cambiado de signo y dividido por uno de los coeficientes de la tabla). Así, los coeficientes b_i de la tercera fila se obtienen mediante las expresiones:

Cada uno de dichos coeficientes es el determinante cambiado de signo de la matriz formada por los coeficientes colocados en la primera y segunda fila (dos filas anteriores) de la primera columna y de la  columna a su derecha y dividido por el coeficiente de la primera columna de la fila anterior. De forma análoga, los coeficientes c_i de la cuarta fila se obtienen usando las filas segunda y tercera y así sucesivamente hasta completar la tabla:

En resumen, para obtener cada elemento de una determinada fila se parte de las dos filas inmediatamente anteriores. Se construye, entonces, una “matriz” con la primera columna de dichas filas y la columna de la derecha de la fila del elemento que se esté calculando, se calcula el determinante cambiado de signo, y, finalmente, se divide el resultado por el elemento de la primera columna de la fila inmediatamente anterior.

Una vez construida la tabla, se puede establecer que D(s) es de Hurwitz si y solo si los números de la columna de la izquierda de la tabla son todos positivos. Además, el criterio de Routh-Hurwitz establece que si en dicha columna hay cambios de signo, el número de cambios de signo (observar que no se dice “el número de elemento negativos”) indica el número de raíces del polinomio D(s) que tienen parte real positiva, que en definitiva, no es otra cosa que el número de polos inestables de un sistema si dicho polinomio es el denominador de su función de transferencia.

Entonces, si D(s) es el denominador de una función de transferencia, y dado que es el signo de los elementos de la primera columna de la tabla de Routh construida a partir de dicho polinomio el que determina si dicho sistema es estable o no, y que por ello si uno de dichos elementos pasa de ser positivo a negativo se puede asegurar que el sistema pasa de ser estable a inestable, es lógico pensar que el caso límite se dará cuando el elemento de la primera columna sea nulo (ni positivo ni negativo).

Efectivamente, se puede asegurar que si en la primera columna de la tabla de Routh todos los elementos son positivos y alguno nulo, entonces el sistema tendrá tantos polos en el eje imaginario como cambios haya de nulo a positivo y viceversa al recorrer dicha columna.

Aquí es conveniente recordar que el hecho de que algún polo del sistema esté sobre el eje imaginario (siendo los demás de parte real negativa) no es sinónimo de que sea un sistema críticamente estable, dado que si tiene polos en el origen no lo es (no es un sistema con estabilidad BIBO, esto es, ante entrada acotada la salida no está acotada).

Además, es importante recalcar que si existe algún elemento negativo en la primera columna de la tabla de Routh el sistema es inestable (tiene tantos polos en el semiplano derecho como cambios de signo haya al recorrer la primera columna de la tabla), sin importar los elementos que pueda haber nulos (se consideran positivos para el recuento de cambios de signo), y que éstos no dan ninguna información respecto al número de polos en el eje imaginario.

Finalmente recordar que el criterio de Routh-Hurwitz solo es válido si la ecuación característica es algebraica y todos sus coeficientes son reales, e insistir en que el criterio de Routh-Hurwitz sólo facilita información sobre la estabilidad absoluta del sistema.

5.3.1. Casos Especiales       Ir al Indice

Dado que para calcular todos los coeficientes de la tabla de Routh es necesario dividir por el primer coeficiente de cada fila, si este coeficiente es nulo da lugar a un problema que será necesario solucionar. Pueden surgir dos situaciones diferentes, como son:

Trataremos cada uno de estos casos por separado.

5.3.1.1. Primer caso       Ir al Indice

Si aparece un cero en la primera posición de la fila, los coeficientes de la siguiente fila resultan ∞, se hace imposible continuar con la construcción de la tabla y el criterio de Routh-Hurwitz no es válido. Para solucionar este problema basta con multiplicar el polinomio D(s) por el factor (s+a), donde a es un número real positivo, y construir normalmente la tabla de Routh para el nuevo polinomio D′(s)=D(s)·(s+a).

Por ejemplo, si D(s)=s⁴+2s³+2s²+4s+1 es el polinomio denominador de la función de transferencia de un sistema lineal, la tabla es:

Multiplicando el polinomio D(s), por ejemplo, por el binomio (s+a) con a=1, se obtiene el nuevo polinomio D′(s)=D(s)(s+1)=s⁵+3s⁴+4s³+6s²+5s+1, y la tabla de Routh es:

Como en la primera columna hay dos cambios de signo, el polinomio D′(s) tiene dos raíces con parte real positiva. Evidentemente, el polinomio D(s) también posee dos raíces con parte real positiva puesto que D′(s) tiene las raíces de D(s) más la raíz correspondiente al binomio (s+1), que tiene parte real negativa. En consecuencia, habrá dos polos del sistema en la región real positiva del plano s.

5.3.1.2. Segundo caso       Ir al Indice

Es el caso en el que todos los coeficientes de un fila de la tabla de Routh son cero. Indica que pueden existir una o más de las siguientes condiciones:

Será necesario hacer algunas modificaciones para construir la tabla. En primer lugar habrá que obtener la que se define como “ecuación auxiliar”. Dicha ecuación se construye de la siguiente forma: Su orden será el orden de la fila inmediatamente superior a la fila de ceros en la tabla de Routh, y sus coeficientes los de dicha fila. Hay que recordar que las potencias del polinomio son alternas, empezando por la mayor. La ecuación auxiliar es siempre de orden par (siempre y cuando no existan raíces en el origen).

Para corregir la situación creada por la existencia de la fila de ceros se toma la primera derivada respecto a s de la ecuación auxiliar, y se reemplaza la fila de ceros por los coeficientes de la ecuación resultante de derivar la ecuación auxiliar.

Por ejemplo, si D(s)=s⁴+2s³+3s²+2s+2 es el denominador de la función de transferencia de un sistema lineal, la tabla de Routh es:

En este caso la ecuación auxiliar es A(s)=2s²+2 y su derivada =4s, cuyos coeficientes reemplazan la fila de ceros:

Como no hay coeficientes de signo negativo en la primera columna de la tabla de Routh y considerando el coeficiente nulo que ha aparecido en la fila s¹ existen 2 cambios de positivo a nulo y viceversa. Por tanto, el polinomio D(s) tiene dos raíces con parte real nula y el resto con parte real negativa.