Descripción externa de un sistema dinámico

Se detallan tres formas diferentes (ecuaciones diferenciales, función de transferencia y respuesta impulso), y la relación entre ellas, de representar matemáticamente un sistema físico lineal desde un punto de vista externo, esto es, únicamente desde la relación entrada-salida del sistema. Se tratan, también, de forma superficial los sistemas multivariables, así como los sistemas con condiciones iniciales no nulas. Se presenta una forma de representar gráficamente los sistemas de control: los diagramas de bloques. Por último, se da una breve referencia a la linealización de sistemas no lineales.

4.1. Introducción      Ir al Indice

La primera necesidad que surge a la hora de realizar el control de un proceso es la de disponer de un modelo matemático que describa con suficiente exactitud el comportamiento del mismo. Esta fase es una de las más delicadas a la hora de abordar un proyecto de control de procesos. Si el modelo matemático que se toma no representa de forma correcta al sistema, todo el desarrollo del diseño que posteriormente se haga no dará en la práctica los resultados deseados.

En general, dada una planta, se pueden estudiar las leyes físicas que gobiernan su funcionamiento y expresar dichas leyes mediante relaciones matemáticas. Teniendo en cuenta que durante este proceso se habrán tenido que realizar aproximaciones y simplificaciones, a la larga existirá una diferencia entre el modelo y la planta real.

El objetivo deberá ser que ese error sea lo más pequeño posible, lo que nos obligará a comparar los comportamientos del sistema real y del modelo y modificar este último mientras el error no esté dentro de unos rangos permisibles.

Una vez obtenido un modelo más o menos correcto se puede simular su comportamiento y realizar el diseño del control sobre él, sin olvidar que los resultados obtenidos por simulación habrá que ajustarlos para el sistema real. Solo con la experiencia se podrán resolver todos estos problemas.

Desde un punto de vista externo un sistema se puede considerar como una "caja negra" (Figura 4.1) con una o varias entradas que pueden manipularse de alguna manera para gobernar el comportamiento de una o varias variables.

Dejando a un lado todas las cuestiones relacionadas con la estructura interna del sistema y atendiendo al mismo desde sus atributos externos, el sistema estará totalmente especificado si es posible conocer la función salida que corresponde a cada posible función de entrada. Es decir, desde un punto de vista externo el sistema queda totalmente especificado dando todas las parejas posibles (u(.),y(.)), donde y(.) es la función salida correspondiente a la entrada u(.).

Esta definición implica que la salida del sistema en un momento dado dependerá no solo del valor de la entrada en dicho instante, sino también de cómo ha evolucionado hasta ese instante, pero nunca de valores futuros (Principio de Causalidad). Implica también que a una función de entrada le corresponde una única función de salida.

Se van a presentar tres formas básicas mediante las cuales se puede representar de forma externa un sistema, así como la relación existente entre cada una de ellas:

1. Ecuaciones diferenciales.
2. Función de transferencia.
3. Respuesta impulso.

Se estudiará también un método de representación gráfica: el diagrama de bloques

4.2. Ecuaciones diferenciales y Función de Transferencia      Ir al Indice

La primera forma de representar la relación entrada-salida de un sistema es mediante la ecuación diferencial que relaciona las variables de entrada y salida del mismo.

Sea un sistema lineal con una sola variable de entrada (independiente) y una sola de salida (variable dependiente) cuya relación puede representarse por la siguiente ecuación diferencial de orden n y de coeficientes constantes:

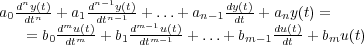(4.1)

donde y(t) es la variable de salida, u(t) la variable de entrada, y los coeficientes a_i, b_j son reales y constantes, para i 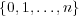y j .

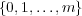La ecuación diferencial es una representación completa del comportamiento del sistema, esto es, especificada la entrada y las condiciones iniciales, la respuesta y(t) se obtiene resolviendo la ecuación diferencial. En particular, la ecuación diferencial queda totalmente determinada por sus coeficientes: n, m, a_i y b_j.

La representación mediante ecuaciones diferenciales es engorrosa y poco útil en la mayoría de los casos, por lo que se va a usar otro método más sencillo y práctico de representación. Aplicando la transformada de Laplace a ambos lados de la ecuación diferencial y suponiendo nulas las condiciones iniciales se obtiene:

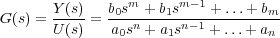
a lo que se denomina función de transferencia del sistema.

Se define por tanto la función de transferencia de un sistema como el cociente de las transformadas de Laplace de la salida y la entrada cuando las condiciones iniciales son nulas (Figura 4.2). Para el tipo de sistemas que se van a estudiar la función de transferencia será siempre el coeficiente de dos polinomios. Más adelante se le dará una interpretación física.

Como características generales de las funciones de transferencia se puede decir:

1. La función de transferencia caracteriza totalmente a la planta desde un punto de vista externo, puesto que contiene toda la información concerniente a los coeficientes de la ecuación diferencial original, y por lo tanto es posible reconstruir ésta fácilmente.
2. Por otro lado permite hallar la salida del sistema para una entrada u(t). Para ello basta calcular U(s) y hacer:
   
   

   Esta forma de operación es en general más sencilla que resolver la ecuación diferencial original.

3. La función de transferencia depende exclusivamente de la planta y no de la entrada a la que está sometida ni de las condiciones iniciales. El hecho de que no dependa de las condiciones iniciales es simplemente por que se han considerado éstas por definición nulas. La función de transferencia presenta n polos y m ceros. Esto se ve más claramente si se representa factorizada la función de transferencia:
   
   

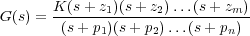
   Los ceros son los valores que hacen nulo el numerador de la función de transferencia, es decir, s=-z_j para j 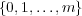y los polos son los valores que anulan su denominador, es decir, s=-p_i para i 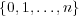. Como se verá más adelante el conocimiento de los n polos va a dar información completa de la dinámica del sistema, esto es, si es estable, si la salida presenta oscilaciones, etc. La ecuación que se obtiene de igualar el denominador de la función de transferencia a cero se denomina ecuación característica y por lo tanto sus raíces son los polos del sistema.

4. Es importante darse cuenta que para que un sistema sea causal se debe verificar que m ≤ n. Para verlo supongamos una función de transferencia de la forma:
   
   

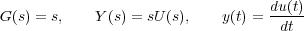
   Esto implica que la salida es la derivada de la entrada, que está en contradicción con el principio de causalidad, ya que la derivada lleva consigo una anticipación. Si u(t) = t, se tiene que y(t) = 1 y por lo tanto en el instante inicial la salida toma un valor diferente de cero mientras la entrada todavía es nula, o sea, existe salida sin existir todavía excitación, lo cual es incompatible con el principio de causalidad.

5. Hay que notar que la ecuación diferencial no representa exactamente al sistema, sino a la relación entrada-salida. En este sentido, dos sistemas de diferente naturaleza pueden tener la misma ecuación diferencial representando su relación entrada-salida.

4.2.1. Sistemas multivariables       Ir al Indice

Para sistemas multivariables lineales puede aplicarse el principio de superposición calculando una función de transferencia para cada par de valores entrada-salida, tal como se refleja en la Figura 4.3 .

Si existen m entradas, cada una de las cuales afecta a las n salidas del sistema, serán necesarias n * m funciones de transferencia para describir el comportamiento del mismo. Dichas funciones de transferencia tendrán todas el mismo denominador (igual ecuación característica) y por lo tanto mismo modo transitorio. Los numeradores serán sin embargo diferentes, variando con ello las magnitudes de las respuestas y también los valores que adquieren las variables de salida del sistema en régimen estacionario.

La función de transferencia de una relación entrada-salida cualquiera, por ejemplo la entrada j y la salida i se define como:

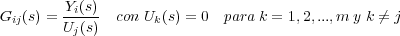
Si se desea obtener el valor de la señal de salida i para el conjunto de las m entradas, dado que el sistema es lineal y por ello cumple el principio de superposición, se podrán sumar todas las contribuciones que cada una de las entradas tiene en la salida i. Esto es, el valor de la salida i para el conjunto de las m entradas se obtendrá como suma de las respuestas particulares a todas y cada una de ellas:

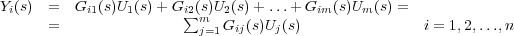
Esta ecuación puede expresarse también en forma matricial mediante la relación:

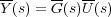
siendo

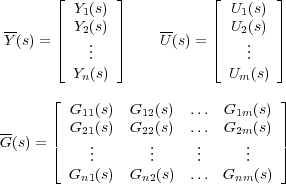
donde la matriz Y(s) es de orden (nx1), U(s) de orden (mx1) y G(s), denominada matriz de función de transferencia o matriz de transferencia del sistema, de orden (nxm).

4.2.2. Sistemas con condiciones iniciales no nulas      Ir al Indice

La función de transferencia del sistema se ha definido como el cociente de las transformadas de Laplace de la salida y la entrada, para condiciones iniciales nulas. Bajo este supuesto las funciones de transferencia del sistema representan exclusivamente el comportamiento dinámico del mismo respecto a una condición de equilibrio determinada (el sistema se haya en reposo o equilibrio en el instante inicial, que es el momento en que se aplica la señal de excitación).

Sin embargo, puede suceder que el sistema no se halle en equilibrio en el instante t = 0, sino que existan unas determinadas condiciones iniciales, bien porque éstas hayan sido introducidas deliberadamente, o porque se haya aplicado una señal de excitación antes del instante t = 0. En tal caso se puede obtener la señal de salida a partir del instante t = 0 aplicando el principio de superposición y considerando la respuesta total del sistema como suma de las respuestas del sistema con condiciones iniciales nulas y la respuesta a las condiciones iniciales en ausencia de señal de entrada.

Partiendo de la ecuación diferencial del sistema, y aplicando la transformada de Laplace a ambos lados de la igualdad, bajo condiciones iniciales no nulas se tendrá:

donde se han considerado nulas las condiciones iniciales correspondientes a la señal de entrada u(t), ya que se trata de hallar la respuesta del sistema a la señal de excitación a partir del instante t = 0.

Despejando Y(s) se obtiene:

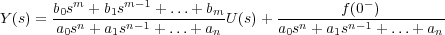
donde el operador que multiplica a U(s) en el primer sumando es la función de transferencia G(s) del sistema y el segundo término es el denominado operador de condiciones iniciales, quedando la expresión de la salida:

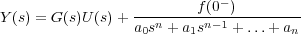
Si en esta ecuación se conoce la transformada U(s) de la señal de entrada u(t) al sistema, se puede obtener directamente la transformada Y(s) de la señal de salida y(t) con solo conocer la función de transferencia G(s) del sistema y el operador de condiciones iniciales.

4.3. Representación mediante la respuesta impulso      Ir al Indice

En el apartado anterior se han visto dos formas de representar externamente un sistema. Se ha visto también que la relación entre ambas era la Transformada de Laplace. Veremos ahora la tercera forma de representar un sistema: la respuesta impulso.

En primer lugar, se verá una definición de la misma y se verá que caracteriza completamente la relación entrada-salida del sistema. Posteriormente se verá la relación que existe entre esta representación y las dos anteriores.

Si suponemos que el sistema está en reposo inicialmente (condiciones iniciales nulas), es correcto escribir que:

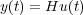(4.2)

donde H es un cierto operador que especifica unívocamente la salida y(t) en función de la entrada u(t).

Si consideramos que u(t) es la entrada al sistema, vamos a buscar una aproximación de la misma como suma de funciones pulso δ_Δ(t - t_i) (Figura 4.4). Como se puede ver en la figura, la señal u(t) se puede aproximar por sucesivos tramos rectos. Cada uno de los tramos rectos lo podemos representar por u(t_i)δ_Δ(t-t_i)Δ, y toda la función de entrada puede escribirse:

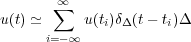
Utilizando esta expresión, y teniendo en cuenta que el sistema es lineal, se puede obtener una aproximación de la señal de salida en función de las señales pulso:

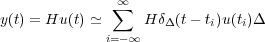
Si calculamos el límite cuando Δ tiende a cero:

siendo δ(t-t₁) =lim_{Δ → 0}δ_Δ(t-t₁) la función impulso o Delta de Dirac. Observando la expresión anterior y la relación fundamental del sistema (4.2<) se define:

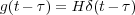
como la respuesta impulso del sistema, que sería la respuesta del sistema cuando la entrada al mismo es la Delta de Dirac. Por lo tanto la señal de salida para la entrada u(t) sería:

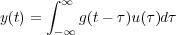
Esta expresión indica que conocida g(t-τ) y u(τ), la salida y(t) queda totalmente especificada. Por tanto, la respuesta impulso g(t-τ) define totalmente el comportamiento del sistema.

Teniendo en cuenta que el sistema es causal, g(t-τ) = 0 para todo t < τ. Además u(τ) = 0 para todo τ < 0, luego

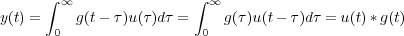
integral que se denomina Integral de Convolución.

Se ha visto, por tanto, que la respuesta del sistema a un impulso aplicado en τ define el comportamiento del mismo. Representamos esa función por g(t - τ) en el caso de sistemas lineales e invariantes en el tiempo. Si τ = 0 (impulso aplicado en cero) entonces la respuesta impulso es g(t).

Veamos la relación entre la respuesta impulso y la función de transferencia de la planta. Sea una planta cuya función de transferencia es G(s) = . Si aplicamos como entrada una función impulso en t = 0 (esto es, u(t)=δ(t), U(s) = 1), la salida será Y (s) = G(s), o sea, y(t) = g(t)=L^-1[Y(s)]=L^-1[G(s)]. Luego se puede establecer que la transformada de Laplace de la respuesta impulso de la planta es la función de transferencia.

En realidad la función impulso δ(t - t₁) es irrealizable, pero podría aproximarse por un pulso de anchura pequeño y gran altura, esto es por la función δ_Δ(t - t₁), donde Δ no es cero pero si muy pequeño. Así si la función de transferencia de un sistema es, por ejemplo, G(s) = 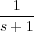la salida ante una entrada impulso δ(t) será:

Y si la entrada no es el impulso ideal sino que es δ_Δ(t - t₁), donde Δ = 0,01, la salida será:

En la Figura 4.5 se puede observar la diferencia entre ambas respuestas del sistema.

Por último, Figura 4.6 muestra un esquema de las diferentes representaciones descritas y la relación entre ellas.

4.4. Diagramas de Bloques      Ir al Indice

A continuación se va a presentar una forma de expresar en forma gráfica las relaciones entrada-salida de los sistemas: los diagramas de bloques.

Conocida la función de transferencia que define el comportamiento de un proceso, se ha visto que se puede calcular la salida Y(s) ante una entrada U(s) mediante la expresión: Y(s) = G(s)U(s), que gráficamente se muestra en la Figura 4.7

Las señales o variables están representadas por flechas que entran o salen de unos bloques que representan las funciones de transferencia de los distintos elementos que componen el sistema. Dos sistemas conectados en serie se representan según el diagrama de bloques de la Figura 4.7.b, donde Y(s)=G(s)U(s) y C(s)=H(s)Y(s).

4.4.1. Elementos fundamentales      Ir al Indice

Los elementos fundamentales que pueden aparecer en un diagrama de bloques se muestran en la Figura 4.8.

4.4.2. Intercambios y reducciones      Ir al Indice

En general dado el esquema de un sistema en forma de diagrama de bloques se trata de reducirlo todo lo posible para poder realizar más fácilmente el estudio de su comportamiento. Para ello serán necesarias una serie de reducciones que se resumen en la Figura 4.9. En esta figura cada uno de los diagramas de bloques de la columna derecha es equivalente a su correspondiente de la columna izquierda.

4.5. Linealización de sistemas      Ir al Indice

La gran mayoría de sistemas físicos son lineales dentro de un rango de las variables que lo componen. Sin embargo, todos los sistemas acaban siendo no lineales si sus variables aumentan sin ningún límite. Por ejemplo, un sistema compuesto por un resorte y una masa es lineal y está descrito por una ecuación lineal, siempre y cuando la masa esté sujeta a pequeñas oscilaciones. Sin embargo, si la amplitud de las oscilaciones se aumentara ilimitadamente, el resorte se estiraría más allá de sus límites y se rompería. Por lo tanto, para cada sistema se debe considerar el problema de la linealidad y el rango de aplicación válidos.

Por otra parte, a la hora de facilitar el trabajo con los modelos matemáticos de sistemas reales es conveniente el escalado de algunas magnitudes. Así, por ejemplo, puede ser interesante trabajar con centímetros si la variable a estudiar del sistema se mueve en valores pequeños (y sería engorroso trabajar en metros). El mismo razonamiento se puede hacer si la variable es el tiempo, así en un proceso de reacción nuclear para facilitar la escritura de sus ecuaciones dinámicas la unidad de tiempo sería conveniente escalarla (en vez de utilizar el segundo habría que poner la unidad de tiempo alternativa al mismo, esto es, el nanosegundo, microsegundo, ...).

Un sistema se define lineal en términos de su excitación o entrada u(t) y de su respuesta y(t), y es lineal si y solo si satisface el principio de superposición y la propiedad de homegeneidad.

Por un lado, el pricipio de superposición establece que si al sistema en reposo se le excita con una señal u₁(t)+u₂(t) debe proporcionar una respuesta y₁(t)+y₂(t), siendo y₁(t) la respuesta que daría el sistema sometido a una excitación u₁(t) e y₂(t) la respuesta del sistema ante una entrada u₂(t) (Figura 4.10).

Por otro lado, la propiedad de homogeneidad establece que si al sistema en reposo se le excita con una señal a·u₁(t), siendo a una constante, debe proporcionar una respuesta ay₁(t), siendo y₁(t) la respuesta que daría el sistema sometido a una excitación u₁(t) (Figura 4.11).

4.5.1. Sistemas no lineales.      Ir al Indice

Como introducción se va a analizar la linealidad de un sistema (Figura 4.12) que viene representado por la relación siguiente:

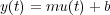
Se puede comprobar que no satisface ni la propiedad de homogeneidad ni el principio de superposición y, por lo tanto, se trata de un sistema no lineal. Sin embargo, puede considerarse lineal respecto de un punto de operación o funcionamiento (u₀,y₀) para cambios pequeños de la entrada y la salida, Δu y Δy, respectivamente.

Supóngase que se ha producido un pequeño desplazamiento del punto de operación inicial (u₀,y₀) y el sistema pasa a estar funcionando en el punto (u,y) donde:

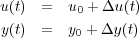
entonces,

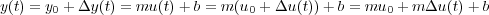
y por tanto se obtiene:

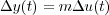
expresión que satisface las condiciones necesarias para que el sistema sea considerado lineal. Esto es, se ha obtenido una relación lineal entre los incrementos de las variables de entrada y de salida (no entre las propias variables) en el entorno del punto de funcionamiento inicial (u₀,y₀).

El caso de linealización de sistemas sometidos a pequeñas perturbaciones es bastante corriente en la práctica, especialmente cuando se trata de sistemas de regulación cuyo objetivo es mantener la variable de salida en un valor nominal fijo. Se va a considerar a continuación el caso general donde la salida y(t) de un sistema está relacionada con su entrada u(t) mediante la relación no lineal siguiente:

representada gráficamente en la Figura 4.13.

Sea P=(u₀,y₀) el punto de funcionamiento nominal, esto es, el punto de funcionamiento en el que va a actuar el sistema. Si en un momento determinado el sistema se ve sometido a una perturbación pasará a actuar en el punto

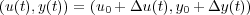
siendo Δu(t) y Δy(t) los efectos debidos a la perturbación, que como se indica serán función del tiempo. Si se desarrolla la salida del sistema en serie de Taylor en el entorno del punto de operación P se obtiene:

expresión en la que todas las derivadas están evaluadas en el punto de funcionamiento nominal P=(u₀,y₀), por lo que serán constantes. Si la perturbación sobre el sistema Δu(t) es pequeña pueden despreciarse los términos de orden superior del desarrollo en serie de Taylor resultando:

donde m es la pendiente en el punto de operación. Finalmente, esta última ecuación puede escribirse como una ecuación lineal de la forma:

Esta ecuación indica que el efecto Δy(t) causado en la salida por la perturbación Δu(t) de la entrada es proporcional a ésta, obteniéndose un modelo matemático lineal para el sistema no lineal original. En definitiva, se ha sustituido la curva de la Figura 4.13  por su tangente en el punto P=(u₀,y₀) de funcionamiento nominal para desviaciones en la entrada muy pequeñas en el entorno del mismo, lo que puede ser una aproximación razonable si Δu(t) es suficientemente pequeño.

Si la variable de salida y(t) depende de diferentes variables de entrada, u₁(t),u₂(t),…,u_n(t), entonces la relación funcional es:

El desarrollo en series de Taylor en el entorno del punto de operación (u₁₀,u₂₀,…,u_n0,y₀), es útil para una aproximación lineal a la función no lineal. Cuando se desprecian los términos de orden más alto, la aproximación lineal queda:

donde u₀ es el punto de operación (u₁₀,u₂₀,…,u_n0). Para que pueda ser aplicada la técnica de linealización en el entorno del punto de trabajo, es necesario que existan todas las derivadas parciales en ese punto, esto es, que sean finitas. Por otra parte las ecuaciones tienen que estar en forma de ecuaciones diferenciales ordinarias antes de realizar la linealización, o sea, habrá que realizar las derivadas parciales antes de la linealización para no olvidarse de términos importantes.

Por último, queda por decidir que valor ha de considerarse "pequeña perturbación" de forma que no lleguen a introducirse errores inaceptables al realizar la linealización.

4.5.2. Sistemas con retardo      Ir al Indice

En los sistemas de regulación automática existen otros elementos, además de los descritos en apartados anteriores, denominados de retardo puro. Son sistemas en los que al producirse una variación en la señal de entrada su efecto no aparece en la señal de salida hasta transcurrido un determinado periodo de tiempo T_r llamado tiempo de retardo. Tal fenómeno se produce, normalmente, en procesos de regulación donde tienen lugar operaciones de transporte de energía o masas a grandes distancias, como por ejemplo en cintas transportadoras, lineas de transporte de energía eléctrica, conducciones de gas o de fluidos de gran longitud, etc. La causa de tal fenómeno es la velocidad limitada con que se propaga la señal desde la entrada hasta la salida del sistema. En sistemas de control digital también aparecen retardos debido al tiempo necesario para realizar los cálculos numéricos.

Desde un punto de vista dinámico, un elemento de retardo puro se comporta como uno proporcional radicando su diferencia exclusivamente en el retardo T_r entre las señales de entrada y de salida, tal como se muestra en la Figura 4.14 .

En el caso concreto representado en la Figura 4.15 de un dispositivo de mezcla de dos soluciones químicas según una proporción c(t) deseada, se dispone de una válvula en la que se realiza la mezcla y un detector de composición del fluido colocado a una distancia d del punto donde se realiza la mezcla. En este sentido, el punto de medición debe estar un poco distante de la válvula para asegurar que la medición sea correcta, ya que la mezcla de las dos soluciones no es instantánea. Entonces, si la velocidad de circulación del fluido es de v m∕s el detector mide la mezcla T_r = seg. después de realizarse.

La ecuación que relaciona la composición medida por el sensor s(t) con la composición que sale de la válvula m(t) es:

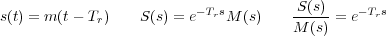
El hecho de que la función de transferencia no sea racional imposibilita el estudio de estos elementos con los métodos de análisis básicos; es decir, observando la posición de los polos y los ceros sobre el plano complejo. Para salvar este inconveniente se realiza una aproximación de la función de transferencia del elemento de retardo puro, de forma que resulte una función algebraica racional. Una de estas aproximaciones es la de Padé:

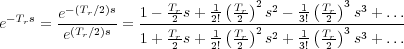(4.3)

 

Figura 4.16: Salida ante entrada escalón unitario de un sistema de primer orden (G(s) = ) con retardo temporal t = 1sg. (línea gruesa), y la salida del mismo sistema con diferentes aproximaciones de Padé del retardo: 2 términos (línea punteada), 3 términos (línea a tramos) y 4 términos (línea continua)

La exactitud de la aproximación depende del número de términos que se tomen en la expresión 4.3. Pero también será importante el valor del retardo T_r, dado que un valor grande del mismo en comparación con la constante de tiempo del sistema obligará a tomar más términos en el desarrollo de Padé para obtener una aproximación aceptable del retardo. Dicho de otra forma, si en T_r segundos al sistema le da tiempo para evolucionar de forma significativa, será necesario tomar más términos de la aproximación que si no fuera así. Como recomendación se aconseja la utilización de la aproximación de orden 3 o superior. Por último, se puede observar en la función de transferencia aproximada que existe una simetría en la posición de polos y ceros respecto del eje imaginario.