Se trata de un primer contacto con los sistemas de control (Automática, Ingeniería de Control o Regulación) con abundantes ejemplos prácticos. Se definen los conceptos que van a utilizarse a lo largo de la asignatura. Finalmente, se da un breve repaso histórico a la Teoría del Control.
Indice del
Capítulo
1.1 Introducción al concepto de control
1.2 Sistemas
de control en lazo abierto
1.3 Sistemas
de control en lazo cerrado
1.4 Visión
histórica de la Teoría de Control
1.5 Clasificación de los sistemas
1.6 Fundamentos de la Teoría de Sistemas
1.6.1 Sistema físico. Modelo. Representación del
modelo
1.6.2 Sistema Dinámico Lineal
La primera vez que se estudia una asignatura de Automática o de Ingeniería de Control no se sabe exactamente a qué se refiere cuando se habla de "sistema de control", y realmente ni siquiera cuando se habla de "control". De hecho, el concepto de control es muy utilizado en diferentes entornos de nuestra vida. Se puede utilizar para referirse a circunstancias puramente humanas (“tengo el control de la situación”), o a una interacción hombre-máquina (conducción de un automóvil, que supone "controlar" el vehículo si no se quiere tener un accidente), y finalmente puede referirse únicamente a máquinas (control de la temperatura de una sala, de la velocidad de giro de un motor, ...).
Se puede decir por tanto que cualquier objeto susceptible de modificar su comportamiento o alguna de sus características puede ser controlado, y por tanto ser considerado como un sistema, y más concretamente un sistema de control, o sistema controlado.
Se puede decir de forma más estricta que un sistema automático de control no es más que un conjunto de dispositivos que acoplados a un proceso, tratan de conseguir que alguna magnitud del mismo varíe en el transcurso del tiempo de alguna forma previamente definida. De acuerdo con esta concepción, un sistema de control puede quedar representado en forma esquemática por una caja que recibe una señal de entrada y transmite una señal de salida (Figura 1.1 ). La señal de entrada al sistema es la conocida como señal de control, señal que es generada por un dispositivo denominado controlador cuya función es la de suministar al sistema la señal adecuada para conseguir que la de salida o variable controlada varíe según las especificaciones de diseño. Un sistema que actúe de esta forma recibe el nombre de sistema de control en lazo abierto.
Suponemos también que podemos aportar calor al líquido del tanque mediante un reostato. La Figura 1.2 lo muestra en forma esquemática.
Si se conocen todos los parámetros que definen el sistema (volumen de fluido en el tanque, calor específico, etc...) así como el caudal y temperatura del fluido que recorre el interior de la tubería, está claro que podremos determinar la cantidad de calor que sería necesario aportar al tanque para mantener la temperatura del fluido en un valor predeterminado o temperatura deseada (supuesta conocida la temperatura ambiente):
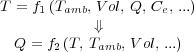
De la misma forma sería posible calcular qué calor deberíamos aportar para que la temperatura del fluido en el tanque variara con el tiempo de una forma determinada. Por lo tanto aportando la cantidad de calor obtenida mediante los cálculos el sistema quedará controlado. Este es un ejemplo de un sistema de control en lazo abierto. Existe una variable de control que es la cantidad de calor aportada por unidad de tiempo y una salida controlada que es la temperatura del fluido contenido en el tanque.
Es necesario destacar que cualquier cambio en las variables del sistema (temperatura ambiente, caudal o temperatura del líquido que circula por la tubería, ...) supondría que el calor suministrado no es adecuado y la temperatura final del fluido no sería la deseada. Lo que supone que sería necesario rehacer todos los cálculos (rehacer el controlador) para obtener un buen control de la temperatura. Es evidente que el sistema sería incapaz de corregir sus propios errores. Esta es una característica general de los sistemas en lazo abierto.
Otros ejemplos de sistemas de control en lazo abierto en los que la acción de control está prefijada son los casos de la tostadora de pan, lavadora automática, etc.
Vamos a ver que la incapacidad de corrección de los errores propios del sistema puede ser evitada con la utilización de los llamados sistemas de control en lazo cerrado o realimentados.
Estos se caracterizan por el hecho de que la variable a controlar (sea temperatura, presión o velocidad) se mide mediante un sensor para poder compararla con el valor que se considera adecuado. De esta forma se sabe si el control está siendo adecuado, y si no, se actúa en consecuencia.
Una primera solución al problema planteado en el ejemplo anterior sería que un operario mida la temperatura del fluido con un termómetro y de acuerdo con las lecturas que hiciera ajustase manualmente el reostato hasta conseguir nuevamente la temperatura deseada. ¿Sigue siendo un control en lazo abierto? Evidentemente hay algo fundamental que ha variado, y es que la variable de control (calor entregado al tanque a través del reostato) depende ahora del valor que tome la variable de salida (temperatura del líquido). Esta es la característica fundamental de un sistema en lazo cerrado o realimentado: la variable de salida es comparada con el valor deseado (o valor de referencia) y de acuerdo con esa comparación se genera una señal de control para que la referencia y la salida lleguen a tomar valores idénticos.
Ahora bien, el sistema con el operador humano descrito no puede considerarse como sistema automático de control, pues el término "automático" excluye necesariamente la existencia de un operador en el sistema de control. De todas formas la experiencia se ha encargado de demostrar que si bien el operador no debe estar incluido en el control sí debe de estar por lo menos cerca de él.
Para realizar de forma automática el control de temperatura del fluido en el tanque podemos disponer de un termopar el cual nos da una tensión que es proporcional a la temperatura del líquido (Figura 1.3 ). Esta tensión se compara con una tensión de referencia asociada a la temperatura que se desea fijar. El resultado de esta comparación será nulo, positivo o negativo, según el fluido tenga la temperatura deseada, inferior o superior a ella. Este resultado puede utilizarse, a través de los dispositivos adecuados, bien para no variar la cantidad de calor suministrada si la comparación ha sido nula o bien para aumentar o disminuir dicha cantidad si la comparación ha sido positiva o negativa.
Un primer esquema de control (Figura 1.4 ) podría ser aquel en el que el reostato se desconecte mientras la temperatura del líquido es superior o igual a la deseada y cuando aquella descienda por debajo de ésta se vuelve a conectar el calentador. Este tipo de control se denomina control Si-No o Todo-Nada (TON).
Este tipo de control no se suele implementar tal como se ha descrito, sino que para evitar unos excesivos encendidos y apagados del calefactor (que supondrían un desgaste que daría resultado con el uso a roturas más que probables) el encendido y apagado siguen la dinámica representada en la gráfica de la Figura 1.5 .
Así, el calefactor no se apaga hasta superar una temperatura superior a la deseada (Tdes + T1), y una vez apagado no se enciende hasta que la temperatura sea inferior a una temperatura inferior a la deseada (Tdes - T1). La anchura del ciclo de histéresis de la gráfica se denomina brecha diferencial o gap, y de su valor dependerá el número de encendidos y apagados y la precisión del control.
|
|
En la Figura 1.6 .a se muestra la evolución temporal de la temperatura que alcanza el fluido para tres valores de la brecha diferencial del control Si-No. Se observa que cuanto menor sea ésta mayor es la precisión del control, pero sin embargo, en contrapartida, el número de veces que se conecta y desconecta el calentador es mayor con el consiguiente mayor desgaste de los materiales.
Si el calefactor permite dar diferentes grados de calor, el esquema de control puede mejorarse de forma que el controlador genera una señal de control que permite regular la cantidad de calor que debe dar el calefactor dependiendo de la señal de error que reciba. Un primer tipo de control puede ser el denominado Proporcional (Figura 1.7 ) en la que el controlador simplemente genera una señal de control propocional a la de error (u(t) = Ke(t)).
Los dispositivos a utilizar pueden ser un amplificador que teniendo como entrada la tensión resultante de la comparación, alimente un motor cuyo eje fija la posición del reostato. De acuerdo con el signo y la magnitud de la salida del operacional, el motor hará desplazar más o menos el reostato hacia uno u otro lado dando así más o menos calor al tanque (Figura 1.3 ).
En la Figura 1.8 se representa una posible respuesta temporal de un sistema de control proporcional de temperatura.
De acuerdo con la definición dada por el American Institute of Electrical Engineers (AIEE) diremos que "un sistema de control realimentado o en lazo cerrado es aquel que tiende a mantener una relación prevista e impuesta por nosotros entre una variable del proceso (la salida) y una entrada de referencia, comparando funciones de esta variables y usando su diferencia como modelo de control".
La representación general para un sistema realimentado se muestra en la Figura 1.9 .a. En la Figura 1.9 .b se representa otro esquema de un sistema realimentado. En él se introduce un nuevo elemento respecto a la representación anterior (Figura 1.9 .a): Se trata de un prefiltro o transductor que permite acondicionar la señal de entrada con la de salida. En aquellos casos (la mayoría) en los que la señal de salida y la realimentada son de diferente naturaleza la introducción de este dispositivo permite la conversión de la señal de referencia en una señal de las mismas dimensiones que la señal que da el sensor. De ese modo, ambas señales podrán ser comparadas para generar la señal de error que será la entrada al elemento de control. En el ejemplo del control de temperatura de los epígrafes anteriores, concretamente en la Figura 1.7 referente al control en lazo cerrado, ya aparece este elemento que en este caso convertía la referencia introducida en ºC (valor deseado para la temperatura del líquido) en voltios, susceptible de ser comparada con la señal que se obtiene del sensor.
Las secciones precedentes nos han servido para distinguir entre sistemas de control en lazo abierto y en lazo cerrado, introduciendo un concepto básico en la Teoría de Control: la Realimentación.
La realimentación no es, en absoluto, un concepto exclusivo de la Ingenieria de Control. Por ejemplo, en una organización social un líder es líder mientras realice de forma satisfactoria los deseos de un grupo. Si falla, es elegido otro líder. En este sistema la salida es el éxito del grupo realizando sus deseos. El éxito actual se compara con el éxito deseado y si coinciden o si el error es pequeño se mantienen las mismas acciones que han llevado a este estado satisfactorio. En caso contrario, es decir, si el error entre lo deseado y lo real es grande, habrá que tomar medidas, como cambiar de líder, de política, etc., es decir, tomar las medidas oportunas para acercarnos a la situación deseada.
Asimismo, muchas de nuestras acciones individuales conllevan el efecto de la realimentación. Por ejemplo, el tomar un objeto con la mano, el conducir un coche (Figura 1.10 ) o la metodología de estudio (Figura 1.11 ) llevan implícito un mecanismo de realimentación.
Debido a que la utilización de la realimentación es evidente tanto en procesos humanos como en la naturaleza, es muy difícil determinar cuándo fue utilizada por primera vez de forma intencionada. Quizás las primeras evidencias claras de la utilización consciente de la realimentación se remontan al siglo I a. de J.C. y aparecen en la obra "Pneumática" de Herón de Alejandría. En ella se muestran unos reguladores de flotación que mantienen la altura de un líquido con un valor determinado mediante el uso de una válvula que cierra el paso de líquido al tanque al alcanzar una determinada altura en forma totalmente análoga a como actúan los reguladores de nivel actuales en las cisternas domésticas. Asimismo, a comienzos de la era cristiana, los árabes emplearon mecanismos de realimentación para la construcción de relojes de agua (Figura 1.12 ).
Sobre el año 1600, Francis Bacon describe un regulador de temperatura ideado por Cornelis Drebbel para sus experimentos de alquimia. Este aparato consistía básicamente en una caja con un fuego en el fondo y encima de éste un compartimento interior que contenía aire o alcohol en un tubo con mercurio. Cuando aumentaba la temperatura, aumentaba la presión dentro del tubo y el mercurio se desplazaba moviendo a su vez una barrita la cual disminuía la apertura de fuego.
En 1750, Meikle idea un dispositivo para orientar de forma óptima las aspas de un molino de viento.
|
|
En 1788 aparece el regulador centrífugo de Watt (Figura 1.13 ). Éste constituye sin duda alguna el ejemplo más clásico de sistema automático de control en lo que podíamos llamar su prehistoria. Además fue de los primeros sistemas de los que se hizo un estudio analítico profundo, que fue realizado por Maxwell en su obra "En governors". Fue diseñado para regular la velocidad de una máquina de vapor. En esencia no es más que un péndulo centrífugo cuyo eje va unido al dispositivo cuya velocidad se desea controlar. La velocidad de giro determina la posición de una leva que a su vez fija la abertura de la válvula de admisión de vapor de la máquina. De esta forma, se consigue mantener la velocidad a un valor determinado incluso si existen perturbaciones introducidas por cambios en el par solicitado a la máquina o en la presión de vapor suministrado a la misma.
A todas estas realizaciones que hemos mencionado les siguieron otras pero con un denominador común: la realimentación. Todos ellos fueron realizados de una forma simplista y en gran parte basándose en la experiencia y por procedimientos de prueba y error.
La Automática dio un paso decisivo con la adopción para el estudio de sus dispositivos de la transformación de Laplace (1779), que permitió realizar un tratamiento analítico sistemático de los dispositivos utilizados. Esta transformación permitió convertir en simples expresiones algebraicas de muy fácil manejo ecuaciones diferenciales lineales con coeficientes constantes que se venían utilizado para modelizar comportamientos de los procesos.
Por otra parte, el desarrollo de la teoría de variable compleja realizado por Cauchy en la misma época contribuyó en forma decisiva al desarrollo de la Automática en el dominio de la transformación de Laplace. Además y como veremos a lo largo del curso, los resultados que se obtengan en el dominio transformado tienen una interpretación física clara y evidente, dándonos información sobre el comportamiento del sistema en el dominio sin transformar, es decir, en el dominio del tiempo.
Con todo, no podemos hablar del establecimiento formal de la Teoría de Control propiamente dicha hasta bien entrado el siglo XX. Desde la aplicación y desarrollo de la transformada de Laplace hasta aproximadamente el comienzo de los años 30 hubo importantes trabajos (como por ejemplo toda la teoría de estabilidad de Lyapunov), pero éstos no fueron específicamente realizados para su aplicación al control. La mayoría de ellos fueron realizados por personas ligadas al campo de la Ingeniería Mecánica y para ser aplicados en ese campo. Sólo cuando fue formalizada la Teoría de Control, todos estos trabajos fueron absorbidos para formar parte de su contenido.
Como primeros trabajos específicos de la Teoría de Control pueden citarse el de Nyquist en 1932 "Regeneratio Theory" y el de Hazen 1934 "Theory of servomechanisms". Es evidente que esta evolución de la Ingeniería no fue casual. La revolución industrial daba lugar a máquinas cada vez más complejas, a la vez que se tendía a realizar productos cada vez más sofisticados. Todo ello exigía que el proceso de fabricación fuera más preciso, rápido, fiel y también más rentable. Todo esto provocó que la Automática tomase cuerpo como Teoría capaz de resolver de una forma estructurada los problemas cada vez más complejos que iban presentándose.
A partir de las fechas antes citadas, empezaron a surgir numerosos trabajos e incluso los primeros libros de texto sobre regulación automática. Como pasó con muchas otras teorías la 2a Guerra Mundial supuso un serio avance del Control debido principalmente a la necesidad de producción rápida y de alta calidad.
Con todo, las exigencias a la Automática fueron aumentando y alrededor del año 1960 nació lo que hoy se conoce como la "Moderna Teoría de Control". Esta teoría está basada en el estudio de las propias ecuaciones diferenciales del sistema, actuando, por tanto, en el dominio temporal, y no en el dominio transformado como ocurría hasta entonces. La idea clave es la utilización de las llamadas variables de estado juntamente con una notación matricial que simplifica notablemente los cálculos a realizar. Tiene por tanto un alto contenido matemático (especialmente matricial) pero permite resolver problemas imposibles de resolver mediante la utilización de la transfornada de Laplace. Hoy en día, los principales trabajos de investigación están dentro de esta linea si bien es necesario señalar que la aplicación real de los resultados que se están obteniendo está aún muy retrasada respecto al desarrollo teórico. Sin embargo, es claro que el avance tecnológico así como el aumento de la necesidad de producir productos más complejos y más baratos llevan irremisiblemente a una aplicación de la Moderna Teoría de Control en los procesos industriales.
No se puede terminar esta relación histórica de la Automática sin dejar de hablar de la influencia del desarrollo de la Informática y la introducción de los ordenadores en el control de sistemas en lo que ha venido en llamarse ”Sistemas de Control Discretos o Digitales”. No es el objetivo de esta sección el hacer una revisión histórica del control de procesos por ordenador pero si es necesario presentarlo debido a la decisiva importancia que tiene actualmente tanto en el campo de la investigación como en el de las realizaciones prácticas. Es importante señalar que la gran potencialidad de los ordenadores a la hora de tratar información numérica (o en otros términos, digital) ha permitido que muchas de las técnicas desarrolladas por la moderna Teoría de Control hayan podido ser llevadas a la práctica.
Es importante señalar en este punto que la mayor parte de los sistemas físicos evolucionan de forma continua con el tiempo y que un ordenador es incapaz de tratar con este tipo de señales: solo puede operar con números. La Electrónica se ha encargado de elaborar los dispositivos adecuados (convertidores A/D y D/A) para convertir señales continuas en una sucesión de valores numéricos y viceversa. De esta forma el esquema general de un control por ordenador será el mostrado en la Figura 1.14 .
En un instante dado el ordenador lee el valor de la salida que le suministra el convertidor A/D. A partir de esa lectura y con lecturas anteriores, el programa de control que lleve el ordenador genera una señal numérica que es convertida en continua por el conversor D/A, generando así una señal de control que entra al sistema. Este proceso se repite en forma generalmente periódica, es decir, cada cierto "intervalo de muestreo".
Notar que en este esquema sólo se lee o se da información del sistema en los "instantes de muestreo" de forma que no sabemos qué ocurre entre dos instantes consecutivos de muestreo. Sin entrar en más detalles sólo señalar que esta forma de operación es la que ha dado origen a la Teoría de Control Digital. Si bien al principio se trató de llevar al campo digital toda la Teoría desarrollada para el continuo, pronto se vieron las inmensas posibilidades que proporcionaba el control digital siendo hoy en día un capítulo de la Automática con más que suficiente entidad.
De entre todo lo expuesto, cabe destacar que la presente asignatura va a estudiar la Teoría Clásica de Control tanto en el dominio temporal como en el transformado mediante la utilización de la transformada de Laplace.
Como veremos más adelante, una de las tareas más importantes a realizar cuando se desea controlar un sistema es la de buscar un modelo matemático de dicho sistema (en general, una ecuación diferencial) que nos permita posteriormente analizar su comportamiento y partiendo de este análisis diseñar el controlador. Por lo tanto, una vez que se ha realizado la modelización del proceso no se manejará al mismo como un ente físico sino como un ente puramente matemático.
Pues bien, una primera clasificación de los sistemas es en base al tipo de modelo al cual responden:
Dependiendo del tipo de señales que se manejan pueden realizarse dos clasificaciones diferentes:
En cuanto a la estructura general del sistema puede hacerse una última clasificación en:
Las posibles combinaciones entre estas clasificaciones sirven para definir de alguna forma a un sistema. En particular, esta asignatura va a centrarse en el estudio de sistemas lineales, continuos, deterministas y generalmente monovariables.
El vocablo sistema es uno de los más extensamente utilizados en la Ciencia apareciendo en casi todos sus campos fundamentales: Física, Química, Economía, Sociología, etc ... Estamos pues ante un concepto muy general y en cierta forma muy impreciso. De momento nos limitaremos a establecer que para nosotros genéricamente un sistema es un objeto, dispositivo o ente donde se manifiesta una relación de tipo causa-efecto.
Debido a la imposibilidad de tener un conocimiento total a priori del comportamiento de un sistema físico, es necesario recurrir a simplificaciones matemáticas del mismo y poder así realizar un análisis del sistema y diseñar el control conveniente. Esta simplificación matemática se denomina modelo del sistema.
Es claro que esta representación no es única. Un sistema podrá ser representado por una ecuación diferencial de orden n, o por n ecuaciones de orden 1, o aplicando la transformada de Laplace, por una relación algebraica. Todas ellas son distintas representaciones para un mismo modelo. En la Figura 1.15 se puede observar el algoritmo de validación del modelo de un sistema físico real.
Es evidente que estamos ante un problema crítico de la Teoría de Sistemas: un mal modelado llevará a que todas las conclusiones que de él obtengamos sean erróneas. Es evidente que si diseñamos un controlador a partir de un modelo erróneo, cuando conectemos ese controlador al proceso real no se comportará como habíamos previsto.
Los dos atributos fundamentales que deben exigirse a un modelo serán entonces:
En la realidad casi nunca se podrá obtener un modelo que corresponda exactamente con el sistema real, aunque en la mayoría de los casos bastará que sus comportamientos sean parecidos en el rango de actuación en el que vaya a trabajar el sistema.
La Teoría de Control, como parte de la Teoría de Sistemas, estudia a los sistemas dinámicos. En todo sistema es posible advertir un conjunto de estimulos (entradas) que actúan sobre él, un conjunto de respuestas (salidas) motivadas por aquéllos y unas observaciones de estas respuestas detectadas bien directamente por nuestros sentidos o por algún sensor artificial. Las entradas pueden ser señales de control elegidas a voluntad y/o señales aleatorias de comportamiento impredecible (perturbaciones). Así mismo pueden existir perturbaciones que actúan sobre la señal contaminando de esta forma la observación. Con todo esto se puede representar un sistema dinámico por el esquema mostrado en la Figura 1.16 . Es evidente que si no existen perturbaciones en la observación entonces ésta coincide con la salida.
Por lo tanto, el modelo de un sistema dinámico debe especificar todas las relaciones existentes entre las señales que intervienen en el proceso considerado. Dado que a lo largo esta asignatura se van a estudiar los sistemas lineales será necesario encontrar una definición de los mismos. Un sistema dinámico es lineal si la salida del mismo cumple el principio de superposición, como se puede ver gráficamente en la Figura 1.17 .