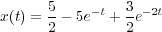Se da un breve repaso a la herramienta matemática que se va a utilizar de forma exhaustiva durante toda la asignatura: La Transformada de Laplace. Previamente se estudia la transformada de Fourier.
2.1 Introducción. El concepto de la
transformación.
2.2 Series
de Fourier. Transformada de Fourier.
2.2.1 La transformada de Fourier
2.3 La
transformada de Laplace
2.4 Teoremas y propiedades básicas
2.5 Transformada inversa
2.6 Aplicación de la transformada de Laplace a la resolución de
ecuaciones diferenciales
La transformación es un concepto muy utilizado para resolver problemas complejos de una manera más simple. Por ejemplo, supóngase que se desea calcular el producto P = a.b de dos números reales a y b. Aplicando logaritmos se tiene:

de manera que si a y b tienen muchas cifras es probable que sea más sencillo y rápido trabajar con sus logaritmos que con las variables en sí. Precisamente, la propiedad anterior es la base de construcción y utilización de las reglas de cálculo de las calculadoras de bolsillo, facilitando su diseño.
Esta filosofía de transformar operaciones en otras más sencillas o más manejables es la que subyace en el método de transformación que se va describir a lo largo de este tema: la transformada de Laplace.
Como primer paso, se estudia una herramienta muy utilizada en muy diversos campos de la ciencia, como son las Series de Fourier y la Transformada de Fourier. En el análisis de sistemas es conveniente, a veces, introducir transformaciones matemáticas que trasladen el problema del dominio del tiempo al de la frecuencia. Una de estas transformaciones es el desarrollo en serie de Fourier, que sirve para analizar funciones periódicas en el tiempo en el dominio de la frecuencia, cuando se cumplen una serie de condiciones.
Una función periódica f(t), de periodo T, acotada en un intervalo que tiene un número finito de máximos y mínimos, así como un número finito de puntos de discontinuidad en un periodo cualquiera, puede ser representada por una serie de Fourier de la siguiente forma:
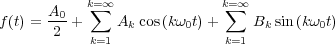
siendo ω0 = 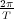 y
y
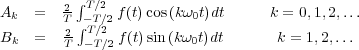
Cuando la función f(t) posee determinadas propiedades de simetría los coeficientes Ak y Bk se simplifican.
La serie de Fourier puede escribirse también en forma de suma de cosenos:
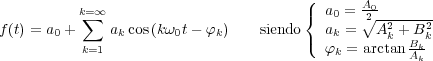
En esta segunda forma la serie de Fourier aparece como una suma de funciones coseno, determinadas por su frecuencia kω0, su amplitud ak y su fase φk. Según este desarrollo, a la función temporal f(t) corresponde una función espectral en el dominio frecuencial, caracterizada por un espectro de amplitudes ak y un espectro de fases φk.
Una tercera variante es la denominada compleja o exponencial, que se obtiene de las ecuaciones de Euler:
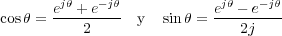
Aplicando estas transformaciones a la función f(t) se obtiene:
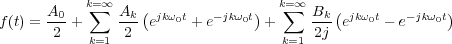
que operando se puede poner:
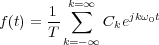
siendo  el
denominado coeficiente complejo de Fourier. Esta expresión para f(t) representa la
serie de Fourier en su forma compleja. Como ejemplo se ve en la Figura
2.1 .b la
forma de los coeficientes complejos de Fourier para un tren de pulsos
(Figura 2.1
.a).
el
denominado coeficiente complejo de Fourier. Esta expresión para f(t) representa la
serie de Fourier en su forma compleja. Como ejemplo se ve en la Figura
2.1 .b la
forma de los coeficientes complejos de Fourier para un tren de pulsos
(Figura 2.1
.a).
Realizando los cálculos se obtiene la expresión de Ck para la función f(t) anterior:
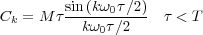
En la Figura 2.1 .b se ha representado Ck en función de la frecuencia. La envolvente de Ck es una curva de la forma sinx∕x (la función sinc) y la distancia entre las líneas del espectro es ω0 = 2π∕T. En este ejemplo Ck es un número real para todo k, por tanto Ck coincide con el espectro de amplitudes y el ángulo de fase es nulo para todas las frecuencias.
Como se ha visto, el desarrollo en serie de Fourier se aplica a funciones periódicas, lo que ayuda en el estudio de sistemas de diferentes tipos (eléctricos, mecánicos, etc.) sometidos a un estímulo de tipo periódico. Sin embargo, en los sistemas de control las funciones más utilizadas no son periódicas sino aperiódicas (un pulso, impulso, etc.) y para todas ellas no es aplicable el desarrollo en serie de Fourier. No obstante, realizando una pequeña modificación se podrán estudiar numerosas funciones aperiódicas con la denominada transformada de Fourier.
Supongamos que queremos transformar la función no periódica representada en la Figura 2.2 .a. Una función de este tipo puede considerarse como uno de los pulsos pertenecientes al tren de pulsos de la Figura 2.1 .a, en el cual sin variar la duración τ del pulso se ha hecho tender el periodo T a infinito. En tales condiciones se puede utilizar el desarrollo en serie de Fourier de f(t), bajo la condición de que el periodo T tienda a infinito, con lo que la separación entre las componentes espectrales ω0 = 2π∕T tenderá a cero. Ck se convierte así en una función prácticamente continua. Y por lo tanto la noción de espectro de frecuencia se convierte en una densidad espectral de frecuencia Ck∕ω0.
Partiendo de la expresión de la función f(t) en función de los coeficientes Ck, y tomando límites cuando T tiende a infinito y ω0 a cero se tiene:
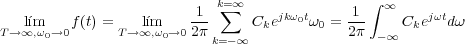
A esta última ecuación se le conoce con el nombre de Integral de Fourier, y en ella puede verse que los valores discretos de las lineas del espectro de Ck se ha transformado en un espectro continuo como se ve en la Figura 2.2 .b. Igualmente la expresión del coeficiente de Fourier Ck se transforma en:
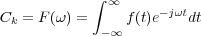
que se define como la transformada de Fourier de la función no periódica f(t) y se representa normalmente como F(ω).
La transformada de Fourier de una función f(t) existe únicamente cuando se cumple la condición de convergencia absoluta (condición necesaria):
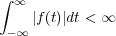
por lo tanto es fundamental antes de calcular cualquier transformada comprobar si se cumple esta condición. Se puede observar que para señales muy usadas en la Teoría de Control, como pueden ser el escalón o la rampa, no existen sus respectivas transformadas de Fourier.
En el caso de la función pulso de altura M y duración finita τ (Figura 2.2 .a), su transformada es:
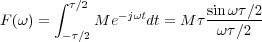
que es la ecuación de la curva mostrada en la Figura 2.2 .b.
Las ecuaciones de f(t) y de su transformada F(ω) se pueden escribir de la forma:
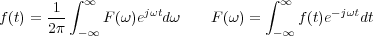
Este par de ecuaciones representa la transformación de una función en el dominio del tiempo f(t) en otra función F(ω) en el dominio de la frecuencia. Dicha transformación se representa de la forma:

La trasformada de Fourier de una función f(t) es una representación de esa función como una suma continua de funciones exponenciales de la forma ejωt, en donde ω es una frecuencia real. Esta interpretación de la transformada de Fourier proporciona un sentido físico a lo que de otra forma sería una transformación matemática abstracta.
Aunque la transformada de Fourier es muy útil como herramienta matemática para la resolución de problemas de Ciencia e Ingeniería, la condición de convergencia definida en el apartado anterior limita notablemente su utilización, especialmente en las técnicas de control, por no tener transformada, como ya se indicó, las funciones clásicas de entrada f(t) = 1, f(t) = t y f(t) = t2 (escalón unitario, rampa y parábola).
Para este tipo de funciones se introduce una modificación en la transformada de Fourier mediante un factor de convergencia; concretamente e-σt, siendo σ un número real y positivo lo suficientemente grande como para garantizar la convergencia absoluta. La nueva transformada viene dada por la expresión:
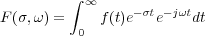
Obsérvese que el límite inferior se ha definido como cero en lugar de -∞; ello es debido a que para valores de σ > 0 el factor de convergencia diverge cuando t tiende a -∞. La nueva transformada, por tanto, no considera la información contenida en f(t) antes de t = 0. Esto no representa un grave inconveniente en las técnicas de control, pues frecuentemente se elige como referencia de tiempo el instante t = 0 (en cualquier caso, se puede introducir una translación temporal). Definiendose s = σ + jω, la ecuación anterior puede escribirse en la forma:
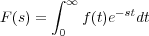
A la función F(s) se le denomina transformada unilateral de Laplace de f(t). Simbólicamente la transformada se representa:
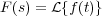
La condición de existencia para la transformada de Laplace es:
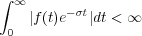
La transformada de Laplace es muy útil para la resolución de ecuaciones diferenciales ordinarias, pues cuando se aplica resulta una ecuación transformada de tipo puramente algebraico, en la variable compleja s, que puede ser fácilmente tratada para obtener la solución deseada como función explícita de s. La solución en función de la variable original t se obtiene aplicando la transformada inversa de Laplace, según la expresión:
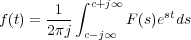
siendo c una constante real tomada mayor que la parte real de los puntos singulares de F(s). Simbólicamente se escribe:
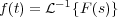
La evaluación de la integral anterior suele presentar bastante dificultad, por lo que normalmente las transformadas inversas se obtienen a partir de tablas de transformadas preparadas al efecto (ver sección 2.5 y apéndice).
Las propiedades más importantes de la Transformada de Laplace son las siguientes:
![[ dnf(t)] L ---n-- = snF(s)- sn-1f(0- )- sn-2f′(0- )- ...- fn-1(0- ) dt](./aut_cap223x.png)
![[∫ ∫ ∫ ] F(s) L ... f(t)dτdτ1...dτn-1 = --n- s](/file.php/83/aut_cap2/aut_cap224x.png)
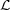
![[f(t- T)]](/file.php/83/aut_cap2/aut_cap225x.png) =
e-sTF(s)
=
e-sTF(s)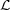
![[∫t ] 0 f2(t- τ)f1(τ)dτ](/ensenanzas-tecnicas/automatica./aut_cap235x.png) = F1(s)F2(s). A la expresión
= F1(s)F2(s). A la expresión ![[∫t ] 0 f2(t- τ)f1(τ)dτ](/file.php/83/aut_cap2//aut_cap235x.png) se la conoce con el nombre de integral de convolución y se puede
representar por f1 * f2.
se la conoce con el nombre de integral de convolución y se puede
representar por f1 * f2.
Otras propiedades interesantes son:
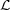
![[e- atf(t)]](/file.php/83/aut_cap2/aut_cap226x.png)
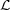
![[f(ct)]](/file.php/83/aut_cap2/aut_cap227x.png) =
=
 F
F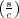
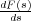 =
-
=
- [tf(t)]
[tf(t)]![∫ c+j∞ L[f1f2] =-1- F2(s- p)F1(p)dp 2πj c-j∞](/file.php/83/aut_cap2/aut_cap236x.png)
Dada una función F(s), la transformada inversa
f(t) se define
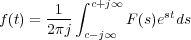
La resolución de esta expresión es en general difícil y requiere la utilización de resultados de la teoría de funciones de variable compleja. Debido a que los sistemas considerados son lineales y de parámetros (o coeficientes) constantes, las funciones transformadas son racionales en la variable s. Se puede, por tanto, descomponer esas expresiones racionales como suma de fracciones simples y teniendo tabuladas las antitransformadas de las funciones elementales, poder hallar la antitransformada de la expresión primitiva. Este será el método más usual de trabajo. Dependiendo del tipo de raíces del denominador (polos) de la función F(s) se operará de una forma u otra:
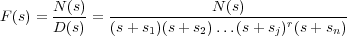
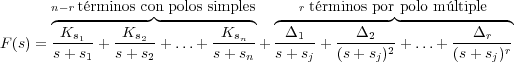
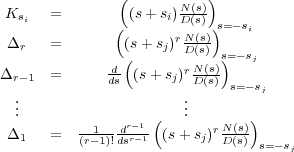
De esta forma se puede obtener la función f(t) realizando la antitransformada de cada sumando con ayuda de las tablas de antitransformadas.
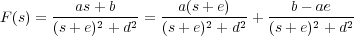
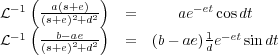
Combinando ambas reglas se puede calcular la transformada de cualquier función F(s), ya que no puede haber otro tipo de polos en el caso de los sistemas lineales con parámetros reales constantes (si existe un polo complejo también existirá su conjugado). En caso de tratarse de un sistema con retardos aparecerán términos no racionales del tipo e-sT cuyo tratamiento requerirá cálculos diferentes.
Como ejemplo de aplicación, se puede partir de una ecuación diferencial
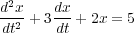
con las condiciones iniciales ẋ(0-) = 2 y x(0-) = -1, donde el simbolo (-) hace mención a las condiciones iniciales "por la izquierda", es decir, al límite t → 0- (por la izquierda). Aplicando la Transformada de Laplace a los dos miembros de la ecuación se obtiene
![s2X(s)- sx(0- )- ˙x(0- )+ 3[sX (s) - x(0- )] +2X (s) = 5 s](/file.php/83/aut_cap2/aut_cap244x.png)
de donde sustituyendo los valores iniciales y descomponiendo en fracciones simples se llega a
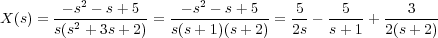
La antitransformada de cada sumando está tabulada, y podemos hallar con facilidad sus transformadas inversas quedando como solución de la ecuación original